题目内容
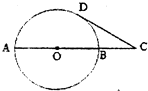
已知AB是圆O的直径,C是AB延长线上一点,CD切圆O于D,CD=4,AB=3BC,则圆O的半径长是 .

考点:与圆有关的比例线段
专题:立体几何
分析:根据已知中:AB是圆O的直径,C是AB延长线上一点,CD切圆O于D,CD=4,AB=3BC,利用切割线定理即可得出.
解答:
解:设圆的半径为r,
∵AB=3BC,
∴2r=3BC.
∵CD切圆O于D,
∴CD2=CB•CA,
∴42=
•(
+2r),
即r2=9,
解得r=3.
故答案为:3
∵AB=3BC,
∴2r=3BC.
∵CD切圆O于D,
∴CD2=CB•CA,
∴42=
| 2r |
| 3 |
| 2r |
| 3 |
即r2=9,
解得r=3.
故答案为:3
点评:本题考查了切割线定理,难度不大,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在R上定义运算?:x?y=x(1-y),若不等式(x-a)?(x+a)<1对任意实数x都成立,则( )
| A、-1<a<1 | ||||
| B、0<a<2 | ||||
C、-
| ||||
D、-
|
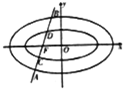 如图所示,已知椭圆C1:
如图所示,已知椭圆C1: