题目内容
a,b为实数,不等式|ax+2|≥|2x+b|的解集为R的充要条件为 .
考点:必要条件、充分条件与充要条件的判断
专题:计算题,不等式的解法及应用,简易逻辑
分析:不等式|ax+2|≥|2x+b|等价于|ax+2|2≥|2x+b|2,化简可得(a2-4)x2+4(a-b)x+(4-b2)≥0,
不等式|ax+2|≥|2x+b|的解集为R可化为(a2-4)x2+4(a-b)x+(4-b2)≥0恒成立;则可得a2-4>0且△=16(a-b)2-4(a2-4)(4-b2)≤0.
不等式|ax+2|≥|2x+b|的解集为R可化为(a2-4)x2+4(a-b)x+(4-b2)≥0恒成立;则可得a2-4>0且△=16(a-b)2-4(a2-4)(4-b2)≤0.
解答:
解:∵|ax+2|≥|2x+b|,
∴|ax+2|2≥|2x+b|2,
∴a2x2+4ax+4≥4x2+4bx+b2,
∴(a2-4)x2+4(a-b)x+(4-b2)≥0.
∴a2-4>0且△=16(a-b)2-4(a2-4)(4-b2)≤0.
∴|a|>2且ab=4.
故答案为:|a|>2且ab=4.
∴|ax+2|2≥|2x+b|2,
∴a2x2+4ax+4≥4x2+4bx+b2,
∴(a2-4)x2+4(a-b)x+(4-b2)≥0.
∴a2-4>0且△=16(a-b)2-4(a2-4)(4-b2)≤0.
∴|a|>2且ab=4.
故答案为:|a|>2且ab=4.
点评:本题考查了绝对值不等式的处理方法及充要条件的求法,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
如图中的直线l1、l2、l3的斜率分别为k1、k2、k3,则( )
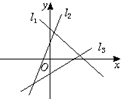

| A、k1<k2<k3 |
| B、k3<k1<k2 |
| C、k3<k2<k1 |
| D、k1<k3<k2 |
用小立方块搭一个几何体,使它的正视图和俯视图如图所示,则它需要的小立方块的个数最多是( )
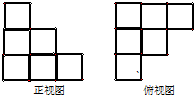

| A、12 | B、13 | C、14 | D、15 |
10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有( )
| A、a>b>c |
| B、b>c>a |
| C、c>a>b |
| D、c>b>a |
函数f(x)=1-|1-2x|,x∈[0,1],函数g(x)=x2-2x+1,x∈[0,1],定义函数F(x)=
那么方程F(x)•2x=1的实根的个数是( )
|
| A、0个 | B、1个 | C、2个 | D、3个 |
给出性质:①最小正周期为π;②图象关于直线x=
对称,则下列四个函数中,同时具有性质①②的是( )
| π |
| 6 |
A、y=sin(2x+
| ||
B、y=sin(2x+
| ||
C、y=sin(2x-
| ||
D、y=sin(x+
|