题目内容
设幂函数y=xa的图象经过点（8，4），则函数y=xa的值域为 ．
考点：幂函数的概念、解析式、定义域、值域
专题：函数的性质及应用
分析：根据幂函数y=xa的图象经过点（8，4）求出a，然后再求函数y=xa的值域即可．
解答：
解：因为幂函数y=xa的图象经过点（8，4），
所以4=8a，
解得：a=
，
所以函数y=x
的值域为：[0，+∞）
故答案为：：[0，+∞）
所以4=8a，
解得：a=
| 2 |
| 3 |
所以函数y=x
| 2 |
| 3 |
故答案为：：[0，+∞）
点评：本题主要考查幂函数的图象与性质．
练习册系列答案
阅读快车系列答案
相关题目
抽查10件产品，设事件A：至少有2件次品，则A的对立事件为（ ）
| A、至多有2件次品 |
| B、至多有1件次品 |
| C、至多有2件正品 |
| D、至多有1件正品 |
命题“?x0∈R，2 x0≤0”的否定为（ ）
| A、?x∈R，2x≤0 |
| B、?x∈R，2x≥0 |
| C、?x∈R，2x＜0 |
| D、?x∈R，2x＞0 |
如图中的直线l1、l2、l3的斜率分别为k1、k2、k3，则（ ）
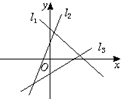
| A、k1＜k2＜k3 |
| B、k3＜k1＜k2 |
| C、k3＜k2＜k1 |
| D、k1＜k3＜k2 |