题目内容
已知f(x)是以5为周期的奇函数,f(-3)=1且tanα=2,则f(20sinαcosα)的值是( )
| A、1 | B、-1 | C、3 | D、8 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:20sinαcosα分母看做“1”,利用同角三角函数间基本关系化简,将tanα的值代入求出值,根据f(x)是以5为周期的奇函数,f(-3)=1,即可确定出所求式子的值.
解答:
解:∵tanα=2,
∴20sinαcosα=
=
=
=8,
∵f(x)是以5为周期的奇函数,f(-3)=1,
∴f(20sinαcosα)=f(8)=f(5+3)=f(3)=-f(-3)=-1.
故选:B.
∴20sinαcosα=
| 20sinαcosα |
| sin2α+cos2α |
| 20tanα |
| tan2α+1 |
| 20×2 |
| 22+1 |
∵f(x)是以5为周期的奇函数,f(-3)=1,
∴f(20sinαcosα)=f(8)=f(5+3)=f(3)=-f(-3)=-1.
故选:B.
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
cos(-2040°)的值为( )
| A、0 | ||||
B、
| ||||
C、
| ||||
D、-
|
某几何体的三视图如图所示,其中俯视图上半部分为半圆,则该几何体的体积为( ) 

A、π+
| ||
B、π+
| ||
| C、π+2 | ||
| D、2π+1 |
已知实数x,y满足:
,则z=2|x|+y的取值范围是( )
|
| A、[0,11] |
| B、[-5,11] |
| C、[-1,11] |
| D、[1,11] |
复数(
)3的共轭复数为( )
| 1+i |
| 1-i |
| A、1 | B、-1 | C、i | D、-i |
二项式(2
-
)6的展开式的常数项是( )
| x |
| 1 | ||
2
|
| A、20 | B、-20 |
| C、15 | D、-15 |
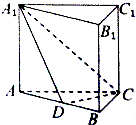 如图,三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,侧棱AA1⊥底面ABC,D为AB的中点,且A1D与底面ABC所成角的正切值为2,则三棱锥A1-ACD外接球的表面积为
如图,三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,侧棱AA1⊥底面ABC,D为AB的中点,且A1D与底面ABC所成角的正切值为2,则三棱锥A1-ACD外接球的表面积为