题目内容
数列{an}是等差数列,数列{bn}满足bn=anan+1an+2(n∈N*),设Sn为{bn}的前n项和.若a12=
a5>0,则当Sn取得最大值时n的值等于 .
| 3 |
| 8 |
考点:数列的求和
专题:点列、递归数列与数学归纳法
分析:根据等差数列的通项公式,以及数列的递推关系,即可得到结论.
解答:
解:设{an}的公差为d,由a12=
a5>0得 a1=-
d,a12<a5,
即d<0,
所以an=(n-
)d,
从而可知1≤n≤16时,an>0,n≥17时,an<0.
从而b1>b2>…>b14>0>b17>b18>…,b15=a15a16a17<0,b16=a16a17a18>0,
故S14>S13>…>S1,S14>S15,S15<S16.
因为a15=-
d>0,a18=
d<0,
所以a15+a18=-
d+
d=
d<0,
所以b15+b16=a16a17(a15+a18)>0,
所以S16>S14,故Sn中S16最大.
故答案为:16
| 3 |
| 8 |
| 76 |
| 5 |
即d<0,
所以an=(n-
| 81 |
| 5 |
从而可知1≤n≤16时,an>0,n≥17时,an<0.
从而b1>b2>…>b14>0>b17>b18>…,b15=a15a16a17<0,b16=a16a17a18>0,
故S14>S13>…>S1,S14>S15,S15<S16.
因为a15=-
| 6 |
| 5 |
| 9 |
| 5 |
所以a15+a18=-
| 6 |
| 5 |
| 9 |
| 5 |
| 4 |
| 5 |
所以b15+b16=a16a17(a15+a18)>0,
所以S16>S14,故Sn中S16最大.
故答案为:16
点评:本题主要考查利用等差数列及等差数列的基本性质是解题基本策略.此题借助了求等差数列前n项和最值的方法,所以在关注方法时,也要关注形成方法的过程和数学思想.

练习册系列答案
相关题目
已知f(x)是以5为周期的奇函数,f(-3)=1且tanα=2,则f(20sinαcosα)的值是( )
| A、1 | B、-1 | C、3 | D、8 |
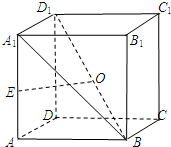 如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为AA1的中点,O为BD1的中点.
如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为AA1的中点,O为BD1的中点. 已知某四棱锥的三视图所示,其中俯视图和左视图都是腰长为4的等腰直角三角形,主视图为直角梯形,则几何体的体积是
已知某四棱锥的三视图所示,其中俯视图和左视图都是腰长为4的等腰直角三角形,主视图为直角梯形,则几何体的体积是