Question

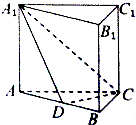如图，三棱柱ABC-A₁B₁C₁中，底面是边长为2的正三角形，侧棱AA₁⊥底面ABC，D为AB的中点，且A₁D与底面ABC所成角的正切值为2，则三棱锥A₁-ACD外接球的表面积为

 

．

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：首先，根据垂直关系，得到∠A₁DA就是A₁D与底面ABC所成的角，然后，设三棱锥A₁-ACD外接球的半径为r，利用等积法求解该r，从而得到其表面积．

解答： 解：如图示：
∵侧棱AA₁⊥底面ABC，
∴∠A₁DA就是A₁D与底面ABC所成的角，
在直角三角形A₁DA中，
tan∠A₁DA=

A1A

AD

=2，
∵底面是边长为2的正三角形，且AD=1，
∴A₁A=2，
设三棱锥A₁-ACD外接球的半径为r，
∵S_△A1DA=

1

2

×1×2=1，
CD=

3

2

×2=

3

，
∴三棱锥A₁-ACD=

1

3

×1×

3

=

3

3

，
V_{三棱锥O-A1CD}+V_{三棱锥O-A1AD}+V_{三棱锥O-A1AC}+V_{三棱锥O-ACD}
=

1

3

×

1

2

×

3

×

5

r+

1

3

×

1

2

×2×1r+

1

3

×

1

2

×2×2r+

1

3

×

1

2

×1×

3

r=

3

3

，
∴r=

2

，
∴三棱锥A₁-ACD外接球的表面积为4πr²=8π．
故答案为：8π．

点评：本题重点考查了空间中垂直关系的判断和应用，掌握等积法在求解几何体的外接球的半径中的应用问题，属于中档题．