题目内容
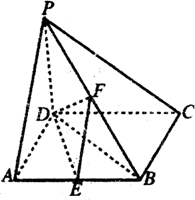 四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,E、F分别是AB、PB的中点.
四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,E、F分别是AB、PB的中点.(1)求证:PA⊥CD;
(2)求三棱锥B-DEF的体积;
(3)二面角E-DF-B的余弦值.
考点:二面角的平面角及求法,棱柱、棱锥、棱台的体积,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(1)由已知得PD⊥CD,CD⊥AD,从而CD⊥平面PAD,由此能证明PA⊥CD.
(2)F到平面BDE的距离h=
PD=1,S△BDE=
×AB×AD=2,由此能求出三棱锥B-DEF的体积.
(3)以D为原点,DA为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,求出平面DEF的法向量和平面BDF的法向量,利用向量法能求出二面角E-DF-B的余弦值.
(2)F到平面BDE的距离h=
| 1 |
| 2 |
| 1 |
| 2 |
(3)以D为原点,DA为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,求出平面DEF的法向量和平面BDF的法向量,利用向量法能求出二面角E-DF-B的余弦值.
解答:
(1)证明:∵PD⊥底面ABCD,CD?平面ABCD,∴PD⊥CD,
∵底面ABCD为正方形,∴CD⊥AD,
∵PD∩AD=D,∴CD⊥平面PAD,
又PA?平面PAD,∴PA⊥CD.
(2)解:∵E、F分别是AB、PB的中点,
∴F到平面BDE的距离h=
PD=1,
S△BDE=
×AB×AD=
×2×2=2,
∴三棱锥B-DEF的体积VB-DEF=VF-BDE=
×h×S△BDE=
.
(3)解:以D为原点,DA为x轴,DC为y轴,DP为z轴,
建立空间直角坐标系,
E(2,1,0),D(0,0,0),P(0,0,2),
B(2,2,0),F(1,1,1),
=(2,1,0),
=(1,1,1),
=(2,2,0),
设平面DEF的法向量
=(x,y,z),
则
,取x=1,得
=(1,-2,1),
设平面BDF的法向量
=(a,b,c),
则
,取a=1,得
=(1,-1,0),
设二面角E-DF-B的平面角为θ,
则cosθ=
=
=
,
∴二面角E-DF-B的余弦值为
.

∵底面ABCD为正方形,∴CD⊥AD,
∵PD∩AD=D,∴CD⊥平面PAD,
又PA?平面PAD,∴PA⊥CD.
(2)解:∵E、F分别是AB、PB的中点,
∴F到平面BDE的距离h=
| 1 |
| 2 |
S△BDE=
| 1 |
| 2 |
| 1 |
| 2 |
∴三棱锥B-DEF的体积VB-DEF=VF-BDE=
| 1 |
| 3 |
| 2 |
| 3 |
(3)解:以D为原点,DA为x轴,DC为y轴,DP为z轴,
建立空间直角坐标系,
E(2,1,0),D(0,0,0),P(0,0,2),
B(2,2,0),F(1,1,1),
| DE |
| DF |
| DB |
设平面DEF的法向量
| n |
则
|
| n |
设平面BDF的法向量
| m |
则
|
| m |
设二面角E-DF-B的平面角为θ,
则cosθ=
|
| ||||
|
|
| 3 | ||||
|
| ||
| 2 |
∴二面角E-DF-B的余弦值为
| ||
| 2 |
点评:本题主要考查直线与平面之间的平行、垂直等位置关系,几何体的体积、二面角的概念、求法等知识,以及空间想象能力和逻辑推理能力.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
若存在x使2•(x-a)>1成立.则a的取值范围是( )
| A、(-∞.+∞) |
| B、(-2,+∞) |
| C、(0.+∞) |
| D、(-1,+∞) |