题目内容

已知递增的等差数列{an}的首项a1=1，且a1、a2、a4成等比数列．
（1）求数列{an}的通项公式an ；
（2）设数列{cn}对任意n∈N*，都有
c1
2
+
c2
22
+…+
cn
2n
=an+1，求c1+c2+…+c2015的值．
考点：数列的求和,等比数列的通项公式,等比数列的性质
专题：等差数列与等比数列
分析：（1）由等比中项的性质列出关于公差d的方程，解方程可得d的值，代入等差数列的通项公式化简；
（2）由（1）化简
c1
2
+
c2
22
+…+
cn
2n
=an+1，令n取n-1代入列出一个式子，两个式子相减即可求出cn，由等比数列的前n项和公式求出c1+c2+…+c2015的值．
解答： 解：（1）设递增的等差数列{an}的公差为d，则d＞0，
∵a1、a2、a4成等比数列，∴a22=a1a4，
∴（1+d）2=1×（1+3d），解得d=1，
∴数列{an}的通项公式为：an=1+n-1=n；
（2）由（1）得，
c1
2
+
c2
22
+…+
cn
2n
=an+1，
则
c1
2
+
c2
22
+…+
cn
2n
=n+1，①
当n≥2时，
c1
2
+
c2
22
+…+
cn-1
2n-1
=n，②
①-②得，
cn
2n
=1，所以cn=2n，
所以c1+c2+…+c2015=2+22+23+…+22015
=
2(1-22015)
1-2
=22016-2．
点评：本题考查等比中项的性质，等差数列的通项公式，以及等比数列的前n项和公式，属于中档题．
练习册系列答案
相关题目
已知f（x）=
3
sinxcosx+3sin2x-
3
2

（1）求f（x）的最小正周期及f（
π
12
）；
（2）求y=f（x）的单调增区间；
（3）当x∈[
π
3
，
5π
6
]时，求y=f（x）的值域．
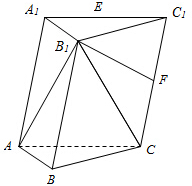已知三棱柱ABC-A1B1C1中，△ABC是以AC为斜边的等腰直角三角形，且B1A=B1C=B1B=AC=2．
（Ⅰ）求证：平面B1AC⊥底面ABC；
（Ⅱ）求B1C与平面ABB1A1所成角的正弦值；
（Ⅲ）若E，F分别是线段A1C1，C1C的中点，问在线段B1F上是否存在点P，使得EP∥平面ABB1A1．
已知
e1
，
e2
是两个不共线的向量，向量
PA
=
e1
+sina•
e2
（-
π
2
＜a＜
π
2
），
PB
=2
e1
-
e2
，
PC
=3
e1
-
5
2
e2
，若A，B，C三点共线，且函数f（x-a）=4cos（x-a）cos（x-2a），则f（x）在[-
π
4
，
π
6
]上的值域为（　　）
A、[-2，
3
+2]
B、[1-
3
，2]
C、[-2
3
，
3
+2]
D、[
3
-1，
3
+2]
等差数列{an}的前n项和Sn
（1）求数列{
Sn
n
}是等差数列
（2）若a1=1，且对任意正整数n，k（n＞k），都有
Sn+k
+
Sn-k
=2
Sn
成立，求数列{an}的通项公式．
（3）记bn=a（a＞0），求证：
b1+b2+…+bn
n
≤
b1+bn
2
．
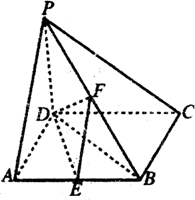四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC=2，E、F分别是AB、PB的中点．
（1）求证：PA⊥CD；
（2）求三棱锥B-DEF的体积；
（3）二面角E-DF-B的余弦值．
已知M、N分别是正方体ABCD-A′B′C′D′的棱BB′和B′C′的中点，求：
（1）MN和CD′所成的角；
（2）MN和AD所成的角．
已知函数f（x）=-x2+ax+b，且f（4）=-3．
（1）若函数f（x）的图象关于直线x=1对称，求函数f（x）在区间[-3，3]上的值域；
（2）若函数f（x）在区间[2，+∞]上递减，求实数b的取值范围．
ABCD是边长为3的正方形，ABEF是矩形，面ABCD垂直于面ABEF，G为EC的中点，求证AC∥面BFG．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网