题目内容
已知函数f(x)=x2+mx+n满足对任意x∈R,有f(x-
)=f(-x-
)成立,并且图象经过点(0,2a-1)(其中a为常数).
(1)试用a表示m、n;
(2)当a<0时,g(x)=
在[e,e2]上有最小值a-1,求实数a的值;
(3)当a=-2时,对任意的x1∈[e,e2],存在x2∈[-
,
]使得不等式f(lnx1)-(4λ-1)(1+lnx1)sinx2≥0成立,求实数λ的取值范围.
| a |
| 2 |
| a |
| 2 |
(1)试用a表示m、n;
(2)当a<0时,g(x)=
| f(lnx) |
| lnx+1 |
(3)当a=-2时,对任意的x1∈[e,e2],存在x2∈[-
| π |
| 6 |
| 2π |
| 3 |
考点:二次函数的性质,函数的最值及其几何意义
专题:函数的性质及应用
分析:(1)根据你对称性得出-
=-
,即m=a,利用f(0)=n=2a-1,即可求解用a表示m、n;
(2)g(x)在[e,e2]上有最小值-3,转化为
≥(4λ-1)sinx2,利用最值,构造最小值的比较即可,即
或
,
| m |
| 2 |
| a |
| 2 |
(2)g(x)在[e,e2]上有最小值-3,转化为
| f(lnx1) |
| lnx1+1 |
|
|
解答:
解:(1)∵函数f(x)=x2+mx+n满足对任意x∈R,有f(x-
)=f(-x-
)成立,
∴-
=-
,即m=a,
∵图象经过点(0,2a-1)(其中a为常数).
∴f(0)=n=2a-1,
∴m=a,n=2a-1,
f(x)=x2+ax+2a-1,
(2)当a<0时,g(x)=
=
=(lnx+1)+
+a-2,
∵x在[e,e2]上,∴g(x)=(lnx+1)+
+a-2,在[e,e2]上单调递增,
∴在[e,e2]上有最小值g(e)=
=a-1,a=-2,
g(x)在[e,e2]上有最小值-3,
∵对任意的x1∈[e,e2],存在x2∈[-
,
]使得不等式f(lnx1)-(4λ-1)(1+lnx1)sinx2≥0成立,
∴不等式f(lnx1)-(4λ-1)(1+lnx1)sinx2≥0,∴
≥(4λ-1)sinx2,
∵x2∈[-
,
],
∴sinx2∈[-
,1],
当4λ-1>0,-
≤(4λ-1)sinx2≤4λ-1
当4λ-1<0,4λ-1≤(4λ-1)sinx2≤-
即
或
,
解得:λ≥1或λ≤-
| a |
| 2 |
| a |
| 2 |
∴-
| m |
| 2 |
| a |
| 2 |
∵图象经过点(0,2a-1)(其中a为常数).
∴f(0)=n=2a-1,
∴m=a,n=2a-1,
f(x)=x2+ax+2a-1,
(2)当a<0时,g(x)=
| f(lnx) |
| lnx+1 |
| (lnx)2+alnx+2a-1 |
| lnx+1 |
| a |
| lnx+1 |
∵x在[e,e2]上,∴g(x)=(lnx+1)+
| a |
| lnx+1 |
∴在[e,e2]上有最小值g(e)=
| 3a |
| 2 |
g(x)在[e,e2]上有最小值-3,
∵对任意的x1∈[e,e2],存在x2∈[-
| π |
| 6 |
| 2π |
| 3 |
∴不等式f(lnx1)-(4λ-1)(1+lnx1)sinx2≥0,∴
| f(lnx1) |
| lnx1+1 |
∵x2∈[-
| π |
| 6 |
| 2π |
| 3 |
∴sinx2∈[-
| 1 |
| 2 |
当4λ-1>0,-
| 4λ-1 |
| 2 |
当4λ-1<0,4λ-1≤(4λ-1)sinx2≤-
| 4λ-1 |
| 2 |
即
|
|
解得:λ≥1或λ≤-
| 1 |
| 2 |
点评:本题综合考虑函数的性质,有关表达式的恒成立问题,转化为最值比较的题目,难度较大,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知四面体OABC各棱长为1,D是棱OA的中点,则异面直线BD与AC所成角的余弦值( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
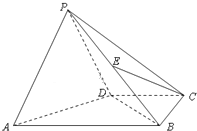 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=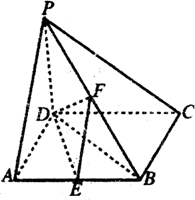 四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,E、F分别是AB、PB的中点.
四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,E、F分别是AB、PB的中点.