题目内容
8.集合M={(x,y)|y=$\sqrt{4-{x}^{2}}$},N={(x,y)|x-y+m=0},若M∩N的子集恰有4个,则m的取值范围是( )| A. | (-2$\sqrt{2}$,2$\sqrt{2}$) | B. | [-2,2$\sqrt{2}$) | C. | (-2$\sqrt{2}$,-2] | D. | [2,2$\sqrt{2}$) |
分析 根据题意,分析可得集合M表示的图形为半圆,集合N表示的图形为直线,M∩N的子集恰有4个,可知M∩N的元素只有2个,即直线与半圆相交.利用数形结合即可得出答案.
解答  解:根据题意,对于集合M,y=$\sqrt{4-{x}^{2}}$,变形可得x2+y2=4,(y≥0),为圆的上半部分,
解:根据题意,对于集合M,y=$\sqrt{4-{x}^{2}}$,变形可得x2+y2=4,(y≥0),为圆的上半部分,
N={(x,y)|x-y+m=0},为直线x-y+m=0上的点,
若M∩N的子集恰有4个,即集合M∩N中有两个元素,则直线与半圆有2个交点,
分析可得:2≤m<2$\sqrt{2}$,
故选:D.
点评 本题考查直线与圆的位置关系,涉及集合子集的个数,关键是分析集合M、N表示的几何图形.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
19.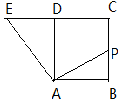 如图,四边形ABCD是正方形,延长CD至E,使得DE=CD,若点P为BC的中点,且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ=( )
如图,四边形ABCD是正方形,延长CD至E,使得DE=CD,若点P为BC的中点,且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ=( )
 如图,四边形ABCD是正方形,延长CD至E,使得DE=CD,若点P为BC的中点,且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ=( )
如图,四边形ABCD是正方形,延长CD至E,使得DE=CD,若点P为BC的中点,且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ=( )| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{5}{2}$ |
20.直线mx-y-2=0与3x-(2+m)y-1=0平行,则实数m为( )
| A. | 1或-3 | B. | -1或3 | C. | -$\frac{1}{2}$ | D. | -1 |
17.已知函数f(x)定义域为R,命题:p:f(x)为奇函数,q:${∫}_{-1}^{1}$f(x)dx=0,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |