题目内容
若圆锥的侧面积是底面积的3倍，则其母线与底面角的大小为 （结果用反三角函数值表示）．
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：由已知中圆锥的侧面积是底面积的3倍，可得圆锥的母线是圆锥底面半径的3倍，在轴截面中，求出母线与底面所成角的余弦值，进而可得母线与轴所成角．
解答：
解：设圆锥母线与轴所成角为θ，
∵圆锥的侧面积是底面积的3倍，
∴
=
=3，
即圆锥的母线是圆锥底面半径的3倍，
故圆锥的轴截面如下图所示：
则cosθ=
=
，
∴θ=arccos
，
故答案为：arccos
∵圆锥的侧面积是底面积的3倍，
∴
| πrl |
| πr2 |
| l |
| r |
即圆锥的母线是圆锥底面半径的3倍，
故圆锥的轴截面如下图所示：
则cosθ=
| r |
| l |
| 1 |
| 3 |
∴θ=arccos
| 1 |
| 3 |
故答案为：arccos
| 1 |
| 3 |
点评：本题考查的知识点是旋转体，其中根据已知得到圆锥的母线是圆锥底面半径的3倍，是解答的关键．
练习册系列答案
英才计划期末调研系列答案
精英口算卡系列答案
相关题目
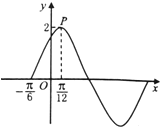已知函数f（x）=Asin（ωx+φ），（ω＞0，A＞0，φ∈（0，
如图，设D是图中边长为2的正方形区域，E是函数y=x3的 图象与x轴及x=±1围成的阴影区域．向D中随机投一点，则该点落入E中的概率为