题目内容
袋中有大小相同的四个球,编号分别为1、2、3、4,从袋中每次任取一个球,记下其编号.若所取球的编号为偶数,则把该球编号改为3后放同袋中继续取球;若所取球的编号为奇数,则停止取球.
(1)求第二次取球后才“停止取球”的概率;
(2)求停止取球时所有被记下的编号之和为5的概率.
(1)求第二次取球后才“停止取球”的概率;
(2)求停止取球时所有被记下的编号之和为5的概率.
考点:相互独立事件的概率乘法公式,互斥事件的概率加法公式
专题:概率与统计
分析:(1)由题意可得,第一次取出的是偶数,第二次取出的为奇数,故所求事件的概率为
×
,计算求得结果.
(2)求出第一次取出的球的编号为2、第二次取出的球的编号为3的概率,再求出第一次取出的球的编号为4 第二次取出的球的编号为1的概率,把这2个概率相加,即得所求.
| 2 |
| 4 |
| 3 |
| 4 |
(2)求出第一次取出的球的编号为2、第二次取出的球的编号为3的概率,再求出第一次取出的球的编号为4 第二次取出的球的编号为1的概率,把这2个概率相加,即得所求.
解答:
解:(1)第二次取球后才“停止取球”,说明第一次取出的是偶数,第二次取出的为奇数,
故第二次取球后才“停止取球”的概率为
×
=
.
(2)若第一次取出的球的编号为2,则第二次取出的球的编号为3,
此时停止取球时所有被记下的编号之和为5的概率为
×
=
.
若第一次取出的球的编号为4,则第二次取出的球的编号为1,
此时停止取球时所有被记下的编号之和为5的概率为
×
=
.
综上可得,停止取球时所有被记下的编号之和为5的概率为
+
=
.
故第二次取球后才“停止取球”的概率为
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
| 8 |
(2)若第一次取出的球的编号为2,则第二次取出的球的编号为3,
此时停止取球时所有被记下的编号之和为5的概率为
| 1 |
| 4 |
| 2 |
| 4 |
| 1 |
| 8 |
若第一次取出的球的编号为4,则第二次取出的球的编号为1,
此时停止取球时所有被记下的编号之和为5的概率为
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 16 |
综上可得,停止取球时所有被记下的编号之和为5的概率为
| 1 |
| 8 |
| 1 |
| 16 |
| 3 |
| 16 |
点评:本题主要考查相互独立事件的概率乘法公式,以及互斥事件的概率加法公式的应用,属于中档题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
如图,在程序框图中输入n-14,按程序运行后输出的结果是( )


| A、0 | B、2 | C、3 | D、4 |
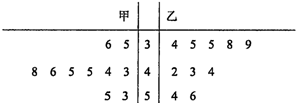
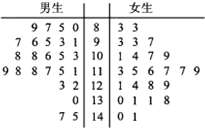 某校高三年级从一次模拟考试中随机抽取50名学生(男、女各25名),将数学成绩进行统计,所得数据的茎叶图如图所示.其中成绩在120分以上(含120分)为优秀.
某校高三年级从一次模拟考试中随机抽取50名学生(男、女各25名),将数学成绩进行统计,所得数据的茎叶图如图所示.其中成绩在120分以上(含120分)为优秀.