题目内容
已知x∈R,则不等式|x+3|-|2x-1|<4的解集为 .
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:通过对自变量x范围的分类讨论,去掉不等式中的绝对值符号,解相应的一次不等式,最后取其并集即可.
解答:
解:当x<-3时,(-x-3)+2x-1<4,解得x<8,取交集得x<-3;
当-3≤x<
时,x+3+2x-1<4,解得x<
,取交集得-3≤x<
;
当x≥
时,x+3-2x+1<4,解得x>0,取交集得x≥
;
综上可得:x∈R.
故答案为:R.
当-3≤x<
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
当x≥
| 1 |
| 2 |
| 1 |
| 2 |
综上可得:x∈R.
故答案为:R.
点评:本题考查绝对值不等式的解法,着重考查分类讨论,去绝对值符号的应用,属于中档题.

练习册系列答案
相关题目
将函数f(x)=sin(2x-
)的图象向右平移
个单位所得到的一条对称轴的方程是( )
| π |
| 6 |
| π |
| 3 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
| D、x=π |

 现将如图所示的5个小正方形涂上红、黄两种颜色,其中3个涂红色,2个涂黄色,若恰有两个相邻的小正方形涂红色,则不同的涂法种数共有
现将如图所示的5个小正方形涂上红、黄两种颜色,其中3个涂红色,2个涂黄色,若恰有两个相邻的小正方形涂红色,则不同的涂法种数共有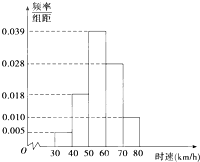 经过随机抽样获得100辆汽车经过某一雷达测速地区的时速(单位:km/h),并绘制成如图所示的频率分布直方图,其中这100辆汽车时速的范围是[30,80],数据分组为[30,40),[40,50),[50,60),[60,70),[70,80].设时速达到或超过60km/h的汽车有x辆,则x等于
经过随机抽样获得100辆汽车经过某一雷达测速地区的时速(单位:km/h),并绘制成如图所示的频率分布直方图,其中这100辆汽车时速的范围是[30,80],数据分组为[30,40),[40,50),[50,60),[60,70),[70,80].设时速达到或超过60km/h的汽车有x辆,则x等于