题目内容
已知a∈R,b∈R,若两集合相等,即{a,
,1}={a2,a+b,0},则a2014+b2014=( )
| b |
| a |
| A、1 | B、-1 | C、0 | D、2 |
考点:集合的相等
专题:集合
分析:由题意,a≠0,则b=0,代入化简求出a,可求a2014+b2014.
解答:
解:∵{a,
,1}={a2,a+b,0},
∴b=0,
∴{a,0,1}={a2,a,0},
则1=a2,
解得,a=-1或a=1(舍去).
则a2014+b2014=1.
| b |
| a |
∴b=0,
∴{a,0,1}={a2,a,0},
则1=a2,
解得,a=-1或a=1(舍去).
则a2014+b2014=1.
点评:本题考查了集合内元素的特征,互异性与无序性,是基础题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
等差数列{an}中,a1=3,a3=9,若ak=243,则k等于( )
| A、79 | B、80 | C、81 | D、82 |
双曲线4x2-3y2=12的焦距等于( )
| A、2 | ||
| B、4 | ||
C、
| ||
D、2
|
曲线y=e2x-x在点(0,1)处的切线方程为( )
A、y=
| ||
| B、y=1 | ||
| C、y=2x-1 | ||
| D、y=x+1 |
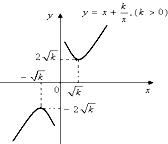 函数f(x)=x+
函数f(x)=x+