题目内容
已知不等式组
，则目标函数z=2x-y的最小值是（ ）
|
| A、8 | B、5 | C、4 | D、1+ln2 |
考点：简单线性规划
专题：不等式的解法及应用
分析：作出可行域，平移直线y=2x可知当直线经过点A（
，-ln2）时，截距最大，z取最小值，代值计算可得．
| 1 |
| 2 |
解答：
解：作出不等式组
所对应的可行域（如图），
变形目标函数可得y=2x-z，平移直线y=2x可知
当直线经过点A（
，-ln2）时，截距最大，z取最小值，
故目标函数z=2x-y的最小值为1+ln2
故选：D
|
变形目标函数可得y=2x-z，平移直线y=2x可知
当直线经过点A（
| 1 |
| 2 |
故目标函数z=2x-y的最小值为1+ln2
故选：D
点评：本题考查简单线性规划，准确作图是解决问题的关键，属中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
函数y=
的定义域是（ ）
| lg(2-4x) |
A、（0，
| ||
B、（-∞，
| ||
C、（0，
| ||
D、（-∞，
|
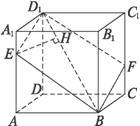如图，正方体ABCD-A1B1C1D1的棱长为a，过其对角线BD1的平面分别与AA1、CC1相交于点E，F，求截面四边形BED1F面积的最小值．已知点M（a，b）（a＞0，b＞0）是圆C：x2+y2=1内任意一点，点P（x，y）是圆上任意一点，则实数ax+by-1为（ ）
| A、一定是负数 | B、一定等于0 |
| C、一定是正数 | D、不确定 |