题目内容
已知点M（a，b）（a＞0，b＞0）是圆C：x2+y2=1内任意一点，点P（x，y）是圆上任意一点，则实数ax+by-1为（ ）
| A、一定是负数 | B、一定等于0 |
| C、一定是正数 | D、不确定 |
考点：直线与圆相交的性质
专题：直线与圆
分析：由条件可得a2+b2＜1，x2+y2=1，可得 x2+y2 +a2+b2＜2，再利用基本不等式求得ax+by＜1，从而得到结论．
解答：
解：由已知点M（a，b）（a＞0，b＞0）是圆C：x2+y2=1内任意一点，可得a2+b2＜1，
再由点P（x，y）是圆上任意一点，可得x2+y2=1，∴x2+y2 +a2+b2＜2．
又∵x2+a2≥2ax，y2+b2≥2yb，
∴x2+y2 +a2+b2≥2ax+2by，当且仅当a=x、b=y时取等号，
∴2ax+2by＜2，∴ax+by＜1，∴ax+by-1＜0，
故选：A．
再由点P（x，y）是圆上任意一点，可得x2+y2=1，∴x2+y2 +a2+b2＜2．
又∵x2+a2≥2ax，y2+b2≥2yb，
∴x2+y2 +a2+b2≥2ax+2by，当且仅当a=x、b=y时取等号，
∴2ax+2by＜2，∴ax+by＜1，∴ax+by-1＜0，
故选：A．
点评：本题主要考查点和圆的位置关系、基本不等式的应用，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示，AB为⊙O的直径，C为⊙O上一点，PA⊥平面ABC，AE⊥PB，垂足为E，AF⊥Pc，垂足为F，求证：PB⊥平面AEF．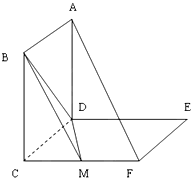
如图，正方形 ABCD 和正方形 CDEF所在平面互相垂直，M为FC的中点．已知不等式组
，则目标函数z=2x-y的最小值是（ ）
|
| A、8 | B、5 | C、4 | D、1+ln2 |