题目内容
20.下列四个函数中,在(0,+∞)上增函数的是( )| A. | f(x)=($\frac{1}{2}$)x-1 | B. | f(x)=log2x-4 | C. | f(x)=3-2x | D. | f(x)=sinx |
分析 根据常见函数的性质判断函数的单调性即可.
解答 解:对于A,函数在(0,+∞)递减,不合题意;
对于B,函数在(0,+∞)递增,符合题意;
对于C,函数在(0,+∞)递减,不合题意;
定义D,函数在(0,$\frac{π}{2}$)递增,在($\frac{π}{2}$,π)递减,不合题意,
故选:B.
点评 本题考查了函数的单调性问题,考查常见函数的性质,是一道基础题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
10.已知等差数列{an}的前n项和为Sn,若$\frac{{a}_{5}}{{a}_{3}}$=$\frac{5}{9}$,则$\frac{{S}_{9}}{{S}_{5}}$=( )
| A. | $\frac{9}{5}$ | B. | 1 | C. | $\frac{3}{5}$ | D. | $\frac{5}{9}$ |
11.为了在运行如图的程序之后输出的值为5,则输入x的所有可能的值是( )


| A. | 5 | B. | -5 | C. | 5或0 | D. | -5或5 |
8.某四棱锥的三视图如图所示,则俯视图的面积为( )
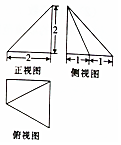

| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |
5.幂函数f(x)=(m2-2m+1)x2m-1在(0,+∞)上为增函数,则实数m的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 1或2 |
9.已知tan($\frac{π}{4}$+α)=$\frac{1}{2}$,则tanα的值为( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{1}{2}$ | D. | -1 |
19.如图,在四棱锥P-ABCD中,底面ABCD是正方形,E为PD中点,若$\overrightarrow{PA}$=$\overrightarrow a$,$\overrightarrow{PB}$=$\overrightarrow b$,$\overrightarrow{PC}$=$\overrightarrow c$,则$\overrightarrow{BE}$=( )

| A. | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\frac{1}{2}$$\overrightarrow c$ | B. | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b-\frac{1}{2}$$\overrightarrow c$ | C. | $\frac{1}{2}\overrightarrow a-\frac{3}{2}\overrightarrow b+\frac{1}{2}$$\overrightarrow c$ | D. | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\frac{3}{2}\overrightarrow c$ |