题目内容
9．已知tan（$\frac{π}{4}$+α）=$\frac{1}{2}$，则tanα的值为（ ）| A． | -$\frac{1}{3}$ | B． | $\frac{1}{3}$ | C． | -$\frac{1}{2}$ | D． | -1 |
分析 利用特殊角的三角函数值及两角和的正切函数公式化简已知即可计算得解．
解答 解：∵tan（$\frac{π}{4}$+α）=$\frac{tan\frac{π}{4}+tanα}{1-tan\frac{π}{4}tanα}$=$\frac{1+tanα}{1-tanα}$=$\frac{1}{2}$，
∴2（1+tanα）=1-tanα，解得：tanα=-$\frac{1}{3}$．
故选：A．
点评 本题主要考查了特殊角的三角函数值及两角和的正切函数公式在三角函数化简求值中的应用，考查了转化思想，属于基础题．
练习册系列答案
相关题目
20．下列四个函数中，在（0，+∞）上增函数的是（ ）
| A． | f（x）=（$\frac{1}{2}$）x-1 | B． | f（x）=log2x-4 | C． | f（x）=3-2x | D． | f（x）=sinx |
4．当x∈（1，+∞）时，下列函数中图象全在直线y=x下方的增函数是（ ）
| A． | $y={x^{\frac{1}{2}}}$ | B． | y=x2 | C． | y=x3 | D． | y=x-1 |
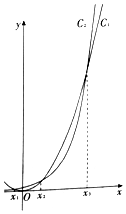函数y=$\frac{1}{4}$•2x和y=$\frac{1}{3}$x2的图象如图所示，其中有且只有x=x1、x2、x3时，两函数值相等，且x1＜0＜x2＜x3，O为坐标原点．