题目内容
19．如图，在四棱锥P-ABCD中，底面ABCD是正方形，E为PD中点，若$\overrightarrow{PA}$=$\overrightarrow a$，$\overrightarrow{PB}$=$\overrightarrow b$，$\overrightarrow{PC}$=$\overrightarrow c$，则$\overrightarrow{BE}$=（ ）
| A． | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\frac{1}{2}$$\overrightarrow c$ | B． | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b-\frac{1}{2}$$\overrightarrow c$ | C． | $\frac{1}{2}\overrightarrow a-\frac{3}{2}\overrightarrow b+\frac{1}{2}$$\overrightarrow c$ | D． | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\frac{3}{2}\overrightarrow c$ |
分析 利用空间向量加法法则求解．
解答 解：∵在四棱锥P-ABCD中，底面ABCD是正方形，E为PD中点，
$\overrightarrow{PA}$=$\overrightarrow a$，$\overrightarrow{PB}$=$\overrightarrow b$，$\overrightarrow{PC}$=$\overrightarrow c$，
∴$\overrightarrow{BE}$=$\frac{1}{2}$（$\overrightarrow{BP}+\overrightarrow{BD}$）=-$\frac{1}{2}$$\overrightarrow{PB}$+$\frac{1}{2}$（$\overrightarrow{BA}+\overrightarrow{BC}$）=-$\frac{1}{2}$$\overrightarrow{PB}$+$\frac{1}{2}$$\overrightarrow{BA}$+$\frac{1}{2}$$\overrightarrow{BC}$
=-$\frac{1}{2}$$\overrightarrow{PB}$+$\frac{1}{2}$（$\overrightarrow{PA}$-$\overrightarrow{PB}$）+$\frac{1}{2}$（$\overrightarrow{PC}$-$\overrightarrow{PB}$）
=-$\frac{3}{2}$$\overrightarrow{PB}$+$\frac{1}{2}$$\overrightarrow{PA}$+$\frac{1}{2}$$\overrightarrow{PC}$=$\frac{1}{2}\overrightarrow{a}$-$\frac{3}{2}\overrightarrow{b}$+$\frac{1}{2}\overrightarrow{c}$．
故选：C．
点评 本题考查向量的求法，是基础题，解题时要认真审题，注意空间向量加法法则的合理运用．
| A． | f（x）=（$\frac{1}{2}$）x-1 | B． | f（x）=log2x-4 | C． | f（x）=3-2x | D． | f（x）=sinx |
| A． | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{5}$=1 | B． | $\frac{{x}^{2}}{13}$-$\frac{{y}^{2}}{13}$=1 | C． | $\frac{{y}^{2}}{5}$-$\frac{{x}^{2}}{5}$=1 | D． | $\frac{{y}^{2}}{13}$-$\frac{{x}^{2}}{13}$=1 |
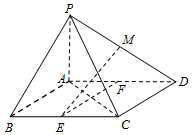如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，∠ABC=45°，PA⊥底面ABCD，AB=AC=PA=2，E、F分别为BC、AD的中点，点M在线段PD上．