题目内容
10．已知等差数列{an}的前n项和为Sn，若$\frac{{a}_{5}}{{a}_{3}}$=$\frac{5}{9}$，则$\frac{{S}_{9}}{{S}_{5}}$=（ ）| A． | $\frac{9}{5}$ | B． | 1 | C． | $\frac{3}{5}$ | D． | $\frac{5}{9}$ |
分析 根据题意和等差数列的性质求出$\frac{{a}_{1}+{a}_{9}}{{a}_{1}+{a}_{5}}$的值，由等差数列的前n和项公式求出$\frac{{S}_{9}}{{S}_{5}}$的值．
解答 解：∵等差数列{an}中，$\frac{{a}_{5}}{{a}_{3}}$=$\frac{5}{9}$，
∴$\frac{{2a}_{5}}{{2a}_{3}}=\frac{{a}_{1}+{a}_{9}}{{a}_{1}+{a}_{5}}$=$\frac{5}{9}$，
∴$\frac{{S}_{9}}{{S}_{5}}$=$\frac{\frac{9}{2}（{a}_{1}+{a}_{9}）}{{\frac{5}{2}（a}_{1}+{a}_{5}）}$=$\frac{9}{5}×\frac{5}{9}$=1，
故选B．
点评 本题考查等差数列的前n项和公式，以及等差数列的性质的灵活应用，考查化简、变形能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
20．当α∈（$\frac{π}{2}$，$\frac{3π}{4}$）时，方程x2sinα-y2cosα=1表示的曲线是（ ）
| A． | 焦点在x轴上的椭圆 | B． | 焦点在y轴上的椭圆 | ||
| C． | 焦点在x轴上的双曲线 | D． | 焦点在y轴上的双曲线 |
1．
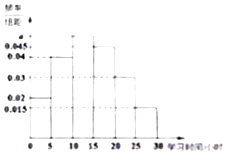某市教育局随机调查了300名高中学生周末的学习时间（单位：小时），制成了如图所示的频率分布直方图，其中学习时间的范围是[0，30]，样本数据分组为，[0，5），[5，10），[10，15），[15，20），[20，25），[25，30]，根据直方图，这300名高中生周末的学习时间不少于15小时的人数是（ ）
某市教育局随机调查了300名高中学生周末的学习时间（单位：小时），制成了如图所示的频率分布直方图，其中学习时间的范围是[0，30]，样本数据分组为，[0，5），[5，10），[10，15），[15，20），[20，25），[25，30]，根据直方图，这300名高中生周末的学习时间不少于15小时的人数是（ ）| A． | 27 | B． | 33 | C． | 135 | D． | 165 |
18．自2017年2月底，90多所自主招生试点高校将陆续出台2017年自主招生简章，某校高三年级选取了在期中考试中成绩优异的100名学生作为调查对象，对是否准备参加2017年的自主招生考试进行了问卷调查，其中“准备参加”、“不准备参加”和“待定”的人数如表：
（I）在所有参加调查的同学中，在三种类型中用分层抽样的方法抽取20人进行座谈交流，则在“准备参加”、“不准备参加”和“待定”的同学中应各抽取多少人？
（II）在“准备参加”自主招生的同学中用分层抽样方法抽取6人，从这6人中任意抽取2 人，求至少有一名女生的概率．
| 准备参加 | 不准备参加 | 待定 | |
| 男生 | 30 | 6 | 15 |
| 女生 | 15 | 9 | 25 |
（II）在“准备参加”自主招生的同学中用分层抽样方法抽取6人，从这6人中任意抽取2 人，求至少有一名女生的概率．
5．设Sn是等差数列{an}的前n项和，且a3=S3=3，则a4+a5=（ ）
| A． | 12 | B． | 9 | C． | 6 | D． | 3 |
20．下列四个函数中，在（0，+∞）上增函数的是（ ）
| A． | f（x）=（$\frac{1}{2}$）x-1 | B． | f（x）=log2x-4 | C． | f（x）=3-2x | D． | f（x）=sinx |