题目内容
12．设集合A={x|a-1＜x＜a+1}，B={x|x＜-1或x＞2}．（1）若A∩B=∅，求实数a的取值范围；
（2）若A∪B=B，求实数a的取值范围．
分析 （1）若A∩B=∅，则$\left\{\begin{array}{l}{a-1≥-1}\\{a+1≤2}\end{array}\right.$，解不等式即可得到所求范围；
（2）若A∪B=B，则A⊆B，则a+1≤-1或a-1≥2，解不等式即可得到所求范围．
解答 解：（1）集合A={x|a-1＜x＜a+1}，B={x|x＜-1或x＞2}，
若A∩B=∅，则$\left\{\begin{array}{l}{a-1≥-1}\\{a+1≤2}\end{array}\right.$
即$\left\{\begin{array}{l}{a≥0}\\{a≤1}\end{array}\right.$，解得：0≤a≤1，
实数a的取值范围时[0，1]；
（2）∵若A∪B=B，∴A⊆B
则a+1≤-1或a-1≥2，
解得：a≤-2或a≥3，
则实数a的取值范围为（-∞，-2]∪[3，+∞）．
点评 本题考查集合的运算，主要是交集、并集，同时考查集合的包含关系，注意运用定义法，考查计算能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
3．将函数$y=sin（x+\frac{π}{6}）$的图象上各点的横坐标变为原来的$\frac{1}{2}$（纵坐标不变），再往上平移1个单位，所得图象对应的函数在下面哪个区间上单调递增（ ）
| A． | $（-\frac{π}{3}，\frac{π}{6}）$ | B． | $（-\frac{π}{2}，\frac{π}{2}）$ | C． | $（-\frac{π}{3}，\frac{π}{3}）$ | D． | $（-\frac{π}{6}，\frac{2π}{3}）$ |
20．下列四个函数中，在（0，+∞）上增函数的是（ ）
| A． | f（x）=（$\frac{1}{2}$）x-1 | B． | f（x）=log2x-4 | C． | f（x）=3-2x | D． | f（x）=sinx |
7．定义在R上的偶函数f（x）满足f（2+x）=f（x），且在[-3，-2]上是减函数，若A、B是锐角三角形ABC的两个内角，则下列各式一定成立的是（ ）
| A． | f（sinA）＜f（cosB） | B． | f（sinA）＞f（cosB） | C． | f（sinA）＞f（sinB） | D． | f（cosA）＞f（cosB） |
4．当x∈（1，+∞）时，下列函数中图象全在直线y=x下方的增函数是（ ）
| A． | $y={x^{\frac{1}{2}}}$ | B． | y=x2 | C． | y=x3 | D． | y=x-1 |
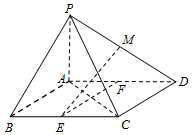如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，∠ABC=45°，PA⊥底面ABCD，AB=AC=PA=2，E、F分别为BC、AD的中点，点M在线段PD上．