题目内容
4.设x∈R,则“1<x<3”是“|x-2|<1”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 由|x-2|<1,解得1<x<3.即可判断出结论.
解答 解:由|x-2|<1,解得1<x<3.
∴“1<x<3”是“|x-2|<1”的充要条件.
故选:C.
点评 本题考查了不等式的解法、简易逻辑,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
15.将函数y=cos(2x+φ)的图象向右平移$\frac{π}{3}$个单位,得到的函数为奇函数,则|φ|的最小值( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
12.某班有60名学生,学号为1~60号,现从中抽取5位同学参加一项活动,用系统抽样的方法确定的抽样号码可能为( )
| A. | 5,10,15,20,25 | B. | 5,12,31,39,57 | C. | 6,16,26,36,46 | D. | 6,18,30,42,54 |
19.设F1、F2分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,P是双曲线C的右支上的点,射线PQ平分∠F1PF2交x轴于点Q,过原点O作PQ的平行线交PF1于点M,若|MP|=$\frac{1}{4}$|F1F2|,则C的离心率为( )
| A. | $\frac{3}{2}$ | B. | 3 | C. | 2 | D. | $\sqrt{3}$ |
9.曲线f(x)=x2+3x-ex在点(0,f(0))处的切线的方程为( )
| A. | y=x-1 | B. | y=x+1 | C. | y=2x-1 | D. | y=2x+1 |
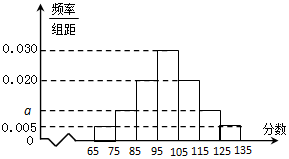 某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图:
某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图: