题目内容
已知直线l1过点A(2,1),B(0,3),直线l2的斜率为-3且过点C(4,2).
(Ⅰ)求l1、l2的交点D的坐标;
(Ⅱ)已知点M(-2,2),N(
,
),若直线l3过点D且与线段MN相交,求直线l3的斜率k的取值范围.
(Ⅰ)求l1、l2的交点D的坐标;
(Ⅱ)已知点M(-2,2),N(
| 15 |
| 2 |
| 7 |
| 2 |
考点:直线的斜率
专题:直线与圆
分析:(I)先求出直线l1和l2所在的直线方程,然后联立两个方程即可求出交点坐标;
(II)首先得出直线l3和线段MN所在直线的方程,然后联立两直线方程即可求出斜率的范围.
(II)首先得出直线l3和线段MN所在直线的方程,然后联立两直线方程即可求出斜率的范围.
解答:
解:(Ⅰ)∵直线l1过点A(2,1),B(0,3),
∴直线l1的方程为
=
,即y=-x+3…(2分)
又∵直线l2的斜率为-3且过点C(4,2)
∴直线l2的方程为y-2=(-3)(x-4),即y=-3x+14…(4分)
∴
,解得
即l1、l2的交点D坐标为(
,-
)…(6分)
说明:在求直线l1的方程的方程时还可以利用点斜式方程或一般式方程形式求解.
(Ⅱ)由题设直线l3的方程为y+
=k(x-
)…(7分)
又由已知可得线段MN的方程为3x-19y+44=0(-2≤x≤
)…(8分)
∵直线l3且与线段MN相交
∴
解得-2≤
≤
…(10分)
得k≤-
或k≥3
∴直线l3的斜率k的取值范围为k≤-
或k≥3.…(12分)
∴直线l1的方程为
| y-1 |
| x-2 |
| 3-1 |
| 0-2 |
又∵直线l2的斜率为-3且过点C(4,2)
∴直线l2的方程为y-2=(-3)(x-4),即y=-3x+14…(4分)
∴
|
|
| 11 |
| 2 |
| 5 |
| 2 |
说明:在求直线l1的方程的方程时还可以利用点斜式方程或一般式方程形式求解.
(Ⅱ)由题设直线l3的方程为y+
| 5 |
| 2 |
| 11 |
| 2 |
又由已知可得线段MN的方程为3x-19y+44=0(-2≤x≤
| 15 |
| 2 |
∵直线l3且与线段MN相交
∴
|
解得-2≤
| 209k+183 |
| 38k-6 |
| 15 |
| 2 |
得k≤-
| 3 |
| 5 |
∴直线l3的斜率k的取值范围为k≤-
| 3 |
| 5 |
点评:本题考查了两直线交点坐标的求法以及直线斜率的应用,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
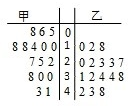 甲乙两组统计数据用茎叶图表示,设甲乙两组数据的平均数分别为
甲乙两组统计数据用茎叶图表示,设甲乙两组数据的平均数分别为. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
sin(-585°)的值为( )
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
已知函数f(x)=sinωx+
cos(π-ωx)(ω>0)的图象的两相邻对称轴间的距离为
,则f(x)的单调递增区间是( )
| 3 |
| π |
| 2 |
A、[kπ-
| ||||
B、[2kπ-
| ||||
C、[kπ-
| ||||
D、[2kπ-
|
二次方程ax2+bx+c=0的两根为-2,3,a<0,那么ax2+bx+c>0的解集为( )
| A、{x|x>3或x<-2} |
| B、{x|x>2或x<-3} |
| C、{x|-2<x<3} |
| D、{x|-3<x<2} |
 (平面几何选做题)
(平面几何选做题)