题目内容
19.已知指数函数y=g(x)满足:g(2)=4,定义域为R的函数f(x)=$\frac{-g(x)+a}{2g(x)+b}$是奇函数.(1)求a,b的值;
(2)判断函数f(x)的单调性(直接写出结论不用证明 )
(3)若对任意的t∈[0,1],不等式f(t2-2t)+f(2t2-k)>0恒成立,求实数k的取值范围.
分析 (1)利用函数奇偶性的性质建立方程关系即可求a,b的值;
(2)函数f(x)是R是上的单调递减函数.
(3)根据函数解析式求出函数的单调性,利用参数分离法进行求解即可
解答 解:(1)设g(x)=mx(m>0,m≠1)∵g(2)=4,∴m2=4,∴m=2,∴g(x)=2x.
∴f(x)=$\frac{-{2}^{x}+a}{2•{2}^{x}+b}$,
∵定义域为R的函数f(x)=$\frac{-g(x)+a}{2g(x)+b}$是奇函数,
∴$\left\{\begin{array}{l}{f(0)=0}\\{f(-1)=-f(1)}\end{array}\right.$,∴$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$.
(2)函数f(x)是R上的单调递减函数.
(3)∵f(2t2-2t)+f(2t2-k)>0对于任意的t∈[0,1]恒成立,
∴f(t2-2t)>-f(2t2-k).
∵定义域为R的函数f(x)是奇函数,
∴f(t2-2t)>f(k-2t2).
∵函数f(x)是R上的减函数,∴t2-2t<k-2t2,
∴k>3t2-2t=2(t-$\frac{1}{3}$)2-$\frac{1}{3}$对于任意的t∈[0,1]恒成立,
令H(x)=3t2-2t t∈[0,1],
只需k>H(x)的最大值即可,
H(x)的最大值为H(1)=1,
∴k>1.
点评 本题主要考查函数奇偶性的应用,以及不等式恒成立,利用函数奇偶性的定义建立方程关系是解决本题的关键.

练习册系列答案
相关题目
9.如图,已知⊙O的半径为5mm,弦AB=8mm,则圆心O到AB的距离是( )
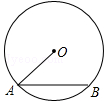

| A. | 1mm | B. | 2mmm | C. | 3mm | D. | 4mm |
10.已知全集U={x|1≤x≤6,x∈Z},集合A={1,3,4},集合B={2,4},则(∁UA)∪B=( )
| A. | {1,2,4,6} | B. | {2,3,4,6} | C. | {2,4,5,6} | D. | {2,6} |
14.三棱锥的棱长均为4$\sqrt{6}$,顶点在同一球面上,则该球的表面积为( )
| A. | 36π | B. | 72π | C. | 144π | D. | 288π |
8.已知a=2${\;}^{\frac{1}{3}}$,b=log3$\frac{1}{2}$,c=log${\;}_{\frac{1}{2}}$$\frac{1}{3}$,则( )
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |