求值:(1)lg52+$\frac{2}{3}$lg8+lg5•lg20+(lg2)2(2)log89•log2732-lg1+log535-log57．题目和参考答案——青夏教育精英家教网—

题目内容

4．求值：
（1）lg5²+$\frac{2}{3}$lg8+lg5•lg20+（lg2）²
（2）log₈9•log₂₇32-（$\sqrt{3-1}$）^lg1+log₅35-log₅7．

分析（1）根据对数的运算性质计算，关键掌握lg2+lg5=1，
（2）根据对数的运算性质和换底公式计算即可．

解答解：（1）原式=2lg5+2lg2+lg5•（1+lg2）+（lg2）²=2+lg5lg2+lg5+（lg2）²=2+lg2（lg5+lg2）+lg5=2+lg2+lg5=3，
（2）原式=$\frac{2lg3}{3lg2}$•$\frac{5lg2}{3lg3}$-1+1=$\frac{10}{9}$

点评本题考查了对数的运算性质和换底公式，属于基础题．

练习册系列答案

时刻准备着寒假作业系列答案

时习之期末加寒假系列答案

寒假作业假期园地中原农民出版社系列答案

15．用数学归纳法证明“$1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2^n}＜f（n）$”时，由n=k不等式成立，证明n=k+1时，左边应增加的项数是（　　）

2^k

12．函数f（x）=$\frac{{x}^{2}}{\sqrt{1-x}}$+lg（2x+1）的定义域为（-$\frac{1}{2}$，1）．

19．已知指数函数y=g（x）满足：g（2）=4，定义域为R的函数f（x）=$\frac{-g（x）+a}{2g（x）+b}$是奇函数．
（1）求a，b的值；
（2）判断函数f（x）的单调性（直接写出结论不用证明）
（3）若对任意的t∈[0，1]，不等式f（t²-2t）+f（2t²-k）＞0恒成立，求实数k的取值范围．

9．已知幂函数f（x）=x^α图象过点$（\sqrt{2}，2）$，则f（9）=81．

16．

已知函数f（x）=-x²+2x+3，x∈[-1，2）
（1）画出函数f（x）的图象；
（2）根据函数f（x）的图象写出函数f（x）的值域．

13．

如图，四棱锥C-ABB₁A₁内接于圆柱OO₁，且A₁A，B₁B都垂直于底面圆O，BC过底面圆心O，M，N分别是棱AA₁，CB₁的中点，MN⊥平面CBB₁．
（1）证明：MN∥平面ABC；
（2）求四棱锥C-ABB₁A₁与圆柱OO₁的体积比．

14．

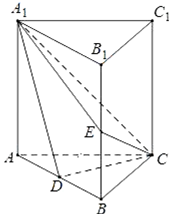如图，直三棱柱ABC-A₁B₁C₁中，D，E分别是AB，BB₁的中点，AA₁=AC=CB=$\frac{\sqrt{2}}{2}$AB．
（Ⅰ）证明：BC₁∥平面A₁CD
（Ⅱ）求点C₁到平面DA₁C的距离．
（Ⅱ）求二面角D-A₁C-E的正弦值．

试题分类