题目内容
9.已知在各项为正的数列{an}中,a1=1,a2=2,log2an+1+log2an=n(n∈N*),则a1+a2+…+a2016-3×21008=-3.分析 根据对数的运算性质,结合题意算出an+1an=2n,从而证出{an}的奇数项、偶数项分别构成以2为公比的等比数列,由此结合等比数列的求和公式即可算出所求式子的值.
解答 解:∵log2an+1+log2an=n
∴log2(an+1an)=n=log22n,可得an+1an=2n
由此可得an+1an+2=2n+1,得$\frac{{a}_{n+2}}{{a}_{n}}$=2
∴a1、a3、…a2015和a2、a4、…、a2016分别构成以2为公比的等比数列
则a1+a3+…+a2015=$\frac{1-{2}^{1008}}{1-2}$=21008-1;a2+a4+…+a2016=$\frac{2(1-{2}^{1008})}{1-2}$=21009-2
∴a1+a2+…+a2016-3×21008
=(21008-1)+(21009-2)-3×21008=3•21008-3-3×21008=-3
故答案为:-3
点评 本题给出各项为正的数列{an}满足的等式,求它的前2016项之和.着重考查了等比数列的通项与求和公式、对数的运算性质和数列递推式的理解等知识,属于中档题.

练习册系列答案
相关题目
1.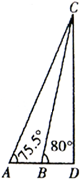 2016年春节期间,小明和小张去上海旅游,参观了东方明珠塔,两人为了测量它的高度,站在A处测得塔尖C的仰角为75.5°,前进38.5m后到达B处,没得塔尖C的仰角为80°,如图所示(其中D为塔底),则东方明珠塔的高度约为( )(参考数据:sin80°≈0.985,sin75.5°≈0.968,sin4.5°≈0.078)
2016年春节期间,小明和小张去上海旅游,参观了东方明珠塔,两人为了测量它的高度,站在A处测得塔尖C的仰角为75.5°,前进38.5m后到达B处,没得塔尖C的仰角为80°,如图所示(其中D为塔底),则东方明珠塔的高度约为( )(参考数据:sin80°≈0.985,sin75.5°≈0.968,sin4.5°≈0.078)
 2016年春节期间,小明和小张去上海旅游,参观了东方明珠塔,两人为了测量它的高度,站在A处测得塔尖C的仰角为75.5°,前进38.5m后到达B处,没得塔尖C的仰角为80°,如图所示(其中D为塔底),则东方明珠塔的高度约为( )(参考数据:sin80°≈0.985,sin75.5°≈0.968,sin4.5°≈0.078)
2016年春节期间,小明和小张去上海旅游,参观了东方明珠塔,两人为了测量它的高度,站在A处测得塔尖C的仰角为75.5°,前进38.5m后到达B处,没得塔尖C的仰角为80°,如图所示(其中D为塔底),则东方明珠塔的高度约为( )(参考数据:sin80°≈0.985,sin75.5°≈0.968,sin4.5°≈0.078)| A. | 456m | B. | 438m | C. | 350m | D. | 471m |
19.不等式2x2-5x-3≥0成立的一个必要不充分条件是( )
| A. | x<0或x>2 | B. | x≥0或x≤-2 | C. | x<-1或x>4 | D. | $x≤-\frac{1}{2}$或x≥3 |
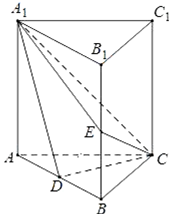 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{\sqrt{2}}{2}$AB.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{\sqrt{2}}{2}$AB.