题目内容
已知双曲线
-
=1的一个焦点为(
,0),一条渐近线方程为y=
x,其中{an}是以4为首项的正数数列.
(Ⅰ)求数列{cn}的通项公式;
(Ⅱ)若不等式
+
+L+
+
<
+logax(a>1)对一切正常整数n恒成立,求实数x的取值范围.
| x2 |
| an |
| y2 |
| an-1 |
| cn |
| ||
| 2 |
(Ⅰ)求数列{cn}的通项公式;
(Ⅱ)若不等式
| 1 |
| c1 |
| 2 |
| c2 |
| n |
| cn |
| n |
| 3•2n |
| 2 |
| 3 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由于双曲线方程为
-
=1的一个焦点为(
,0),可得cn=an+an-1.由于一条渐近线方程为y=
x,可得
=
,即
=2,利用等比数列的通项公式即可得出.
(II)设Tn=
[
+
+
+…+
],利用“错位相减法”、等比数列的前n项和公式可得Tn=
-
-
,故原不等式等价于
-
<
+logax恒成立,化为logax≥0.由于a>1,即可得出.
| x2 |
| an |
| y2 |
| an-1 |
| cn |
| ||
| 2 |
| ||
|
| 2 |
| an |
| an-1 |
(II)设Tn=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
| 2 |
| 3 |
| 1 |
| 3×2n+1 |
| n |
| 3•2n |
| 2 |
| 3 |
| 1 |
| 3×2n+1 |
| 2 |
| 3 |
解答:
解:(Ⅰ)∵双曲线方程为
-
=1的一个焦点为(
,0),
∴cn=an+an-1.
又∵一条渐近线方程为y=
x,
∴
=
,即
=2,
∴an=4×2n-1=2n+1.
∴cn=2n+1+2n=3×2n.
(II)设Tn=
[
+
+
+…+
]①,
Tn=
(
+
+…+
)②,
①-②得,
Tn=
•(
+
+…+
-
)=
×(
-
)=
(1-
),
∴Tn=
-
-
,
故原不等式等价于
-
<
+logax恒成立,
∴logax≥0.
∵a>1,
∴x≥1,
∴实数x的取值范围是[1,+∞).
| x2 |
| an |
| y2 |
| an-1 |
| cn |
∴cn=an+an-1.
又∵一条渐近线方程为y=
| ||
| 2 |
∴
| ||
|
| 2 |
| an |
| an-1 |
∴an=4×2n-1=2n+1.
∴cn=2n+1+2n=3×2n.
(II)设Tn=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 22 |
| 2 |
| 23 |
| n |
| 2n+1 |
①-②得,
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
| n |
| 2n+1 |
| 1 |
| 3 |
| ||||
1-
|
| n |
| 2n+1 |
| 1 |
| 3 |
| 2+n |
| 2n+1 |
∴Tn=
| 2 |
| 3 |
| 1 |
| 3×2n+1 |
| n |
| 3•2n |
故原不等式等价于
| 2 |
| 3 |
| 1 |
| 3×2n+1 |
| 2 |
| 3 |
∴logax≥0.
∵a>1,
∴x≥1,
∴实数x的取值范围是[1,+∞).
点评:本题考查了双曲线的标准方程及其性质、等比数列的通项公式及前n项和公式、“错位相减法”,考查了不等式恒成立的等价转化方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知集合A={x|x<5},B={-1,3,5,7},则A∩B=( )
| A、{-1,3,5} |
| B、{-1,3} |
| C、{3,5} |
| D、{5,7} |
设曲线y=
在点(3,2)处的切线与直线ax+y+1=0垂直,则a=( )
| x+1 |
| x-1 |
| A、2 | ||
| B、-2 | ||
C、-
| ||
D、
|
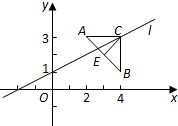 如图,已知点A(2,3),B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.
如图,已知点A(2,3),B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上. 某商场为经营一批每件进价是10元的小商品,对该商品进行为期5天的市场试销.下表是市场试销中获得的数据.
某商场为经营一批每件进价是10元的小商品,对该商品进行为期5天的市场试销.下表是市场试销中获得的数据.