题目内容
有两个不透明的箱子,每个箱子里都装有4个完全相同的小球,球上分别标有数字1,2,3,4,
(1)甲从其中一个箱子中摸出一个球,乙从另一个箱子中摸出一个球,谁摸出的球上标的数字大谁获胜(若数字相同则为平局),求甲获胜的概率;
(2)摸球方法与(1)相同,若规定:两人摸到的球上所标数字相同甲获胜,所标数字不同则乙获胜,这样规定公平吗?
(1)甲从其中一个箱子中摸出一个球,乙从另一个箱子中摸出一个球,谁摸出的球上标的数字大谁获胜(若数字相同则为平局),求甲获胜的概率;
(2)摸球方法与(1)相同,若规定:两人摸到的球上所标数字相同甲获胜,所标数字不同则乙获胜,这样规定公平吗?
考点:概率的应用
专题:应用题,概率与统计
分析:(1)记甲,乙摸出的数字为(x,y);则共有4×4=16种情况,列举出x>y的情况,从而解得.
(2)摸到的球上所标数字相同的情况有(4,4),(2,2),(3,3),(1,1)共4种情况,从而求概率.
(2)摸到的球上所标数字相同的情况有(4,4),(2,2),(3,3),(1,1)共4种情况,从而求概率.
解答:
解:(1)记甲,乙摸出的数字为(x,y);则共有4×4=16种情况,
则x>y的有:(4,1),(4,2),(4,3),(3,2),(3,1),(2,1)共6种情况,
故甲获胜的概率为
=
;
(2)摸到的球上所标数字相同的情况有(4,4),(2,2),(3,3),(1,1)共4种情况,
故甲获胜的概率为
=
,乙获胜的概率为
=
;
故不公平.
则x>y的有:(4,1),(4,2),(4,3),(3,2),(3,1),(2,1)共6种情况,
故甲获胜的概率为
| 6 |
| 16 |
| 3 |
| 8 |
(2)摸到的球上所标数字相同的情况有(4,4),(2,2),(3,3),(1,1)共4种情况,
故甲获胜的概率为
| 4 |
| 16 |
| 1 |
| 4 |
| 12 |
| 16 |
| 3 |
| 4 |
故不公平.
点评:本题考查了古典概型在实际问题中应用,属于中档题.

练习册系列答案
相关题目
复数z=
的实部是( )
| 1-i |
| i |
| A、-2 | B、-1 | C、1 | D、2 |
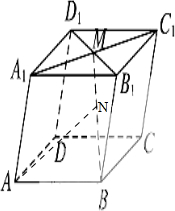 如图,在平行六面体ABCD-A1B1C1D1中,点M为A1C1与B1D1的交点,若
如图,在平行六面体ABCD-A1B1C1D1中,点M为A1C1与B1D1的交点,若| A1B1 |
| a |
| A1D1 |
| b |
| A1A |
| c |
| BN |
| NM |
| AN |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
