题目内容
17.如图,O是坐标原点,M、N是单位圆上的两点,且分别在第一和第三象限,则$|\overrightarrow{OM}+\overrightarrow{ON}|$的范围为[0.$\sqrt{2}$).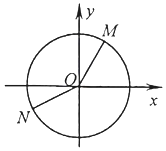
分析 设$\overrightarrow{OM},\overrightarrow{ON}$的夹角为θ,$θ∈(\frac{π}{2},π]$,则cosθ∈[-1,0),$|\overrightarrow{OM}+\overrightarrow{ON}|$2=${\overrightarrow{OM}}^{2}+{\overrightarrow{ON}}^{2}+2\overrightarrow{OM}•\overrightarrow{ON}$=2+2cosθ即可.
解答 解:设$\overrightarrow{OM},\overrightarrow{ON}$的夹角为θ,$θ∈(\frac{π}{2},π]$,则cosθ∈[-1,0),
$|\overrightarrow{OM}+\overrightarrow{ON}|$2=${\overrightarrow{OM}}^{2}+{\overrightarrow{ON}}^{2}+2\overrightarrow{OM}•\overrightarrow{ON}$=2+2cosθ∈[0,2)
$|\overrightarrow{OM}+\overrightarrow{ON}|$的范围为:[0,$\sqrt{2}$),
故答案为[0,$\sqrt{2}$).
点评 本题考查了向量模的取值范围的求解,转化为三角函数求最值,属于基础题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
8.已知sinα-sinβ=1-$\frac{\sqrt{3}}{2}$,cosα-cosβ=$\frac{1}{2}$,则cos(α-β)=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
5.已知复数z=$\frac{2i}{1-i}$,其中i 为虚数单位,则z所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({b>a>0})$的左焦点关于C的一条渐近线的对称点在另一条渐近线上,则C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
6.等差数列的前n项,前2n项,前3n项的和分别为A,B,C,则( )
| A. | A+C=2B | B. | B2=AC | C. | 3(B-A)=C | D. | A2+B2=A(B+C) |
7.点M(0,2)为圆C:(x-4)2+(y+1)2=25上一点,过M的圆的切线为l,且l与l′:4x-ay+2=0平行,则l与l′之间的距离是( )
| A. | $\frac{8}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{28}{5}$ | D. | $\frac{12}{5}$ |