题目内容
平面向量
,
,
满足
=(1,0),
=(1,m),
=(2,n),|
-
|=2,则
•
的最小值为 .
| a |
| b |
| e |
| e |
| a |
| b |
| a |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:计算题,不等式的解法及应用,平面向量及应用
分析:由于|
-
|=2,可得(m-n)2=3.只考虑mn<0.不妨取n>0,m<0.利用向量的数量积运算、基本不等式可得
•
=2+mn=2-(-m)n≥2-(
)2即可得出.
| a |
| b |
| a |
| b |
| -m+n |
| 2 |
解答:
解:由
=(1,m),
=(2,n),|
-
|=2,
则
=2,
即有(m-n)2=3,
只考虑mn<0.不妨取n>0,m<0.
则
•
=2+mn=2-(-m)n≥2-(
)2
=2-
=
.
当且仅当-m=n=
时,取得最小值
.
故答案为:
.
| a |
| b |
| a |
| b |
则
| (1-2)2+(m-n)2 |
即有(m-n)2=3,
只考虑mn<0.不妨取n>0,m<0.
则
| a |
| b |
| -m+n |
| 2 |
=2-
| 3 |
| 4 |
| 5 |
| 4 |
当且仅当-m=n=
| ||
| 2 |
| 5 |
| 4 |
故答案为:
| 5 |
| 4 |
点评:本题考查了向量的数量积运算、基本不等式的性质,考查了分析问题与解决问题的能力,考查了推理能力与计算能力.

练习册系列答案
相关题目
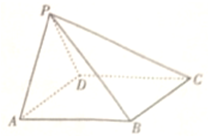 已知四棱锥P-ABCD,侧面PAD⊥底面ABCD,侧面PAD为等边三角形,底面ABCD为棱形且∠DAB=
已知四棱锥P-ABCD,侧面PAD⊥底面ABCD,侧面PAD为等边三角形,底面ABCD为棱形且∠DAB= 如图,M、N是焦点为F的抛物线y2=2px(p>0)上两个不同的点,且线段MN中点A的横坐标为
如图,M、N是焦点为F的抛物线y2=2px(p>0)上两个不同的点,且线段MN中点A的横坐标为