题目内容
已知
=(
sinx,1),
=(cosx,2).
(1)若
∥
,求tan2x的值;
(2)若f(x)=(
-
)•
,求f(x)的单调递增区间.
| a |
| 3 |
| b |
(1)若
| a |
| b |
(2)若f(x)=(
| a |
| b |
| b |
考点:平面向量数量积的运算,平面向量共线(平行)的坐标表示
专题:平面向量及应用
分析:(1)利用向量共线定理、倍角公式即可得出;
(2)利用数量积运算性质、倍角公式、两角和差的正弦公式可得f(x)=(
-
)•
=
•
-
2=sin(2x-
)-
,再利用正弦函数的单调性即可得出.
(2)利用数量积运算性质、倍角公式、两角和差的正弦公式可得f(x)=(
| a |
| b |
| b |
| a |
| b |
| b |
| π |
| 6 |
| 5 |
| 2 |
解答:
解:(1)
∥
⇒2
sinx-cosx=0,
∴tanx=
;
∴tan2x=
=
.
(2)f(x)=(
-
)•
=
•
-
2=
sinxcosx+2-cos2x-4=
sin2x-
-2
=
sin2x-
cos2x-
=sin(2x-
)-
,
令-
+2kπ≤2x-
≤
+2kπ,k∈Z⇒-
+kπ≤x≤
+kπ,k∈Z.
所以f(x)的单调递增区间是[-
+kπ,
+kπ]k∈Z.
| a |
| b |
| 3 |
∴tanx=
| ||
| 6 |
∴tan2x=
| 2tanx |
| 1-tan2x |
4
| ||
| 11 |
(2)f(x)=(
| a |
| b |
| b |
| a |
| b |
| b |
| 3 |
| ||
| 2 |
| 1+cos2x |
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
=sin(2x-
| π |
| 6 |
| 5 |
| 2 |
令-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
所以f(x)的单调递增区间是[-
| π |
| 6 |
| π |
| 3 |
点评:本题考查了向量共线定理、倍角公式、数量积运算性质、两角和差的正弦公式、正弦函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马,现双方各出上、中、下等马各一匹分组分别进行一场比赛,胜两场及以上者获胜,若双方均不知道对方马的出场顺序,则田忌获胜的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
| OA, |
| OB |
| OA |
| OB |
| OM |
| OA |
| ON |
| OB |
| MN |
| 2 |
| 7 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
若函数f(x)唯一的一个零点同时在区间(2,16),(2,8),(2,4)内,那么下列命题中正确的是( )
| A、f(x)在区间(2,3)内有零点 |
| B、f(x)在区间(2,3)或(3,4)内有零点 |
| C、f(x)在区间(3,16)内无零点 |
| D、f(x)在区间(4,16)内无零点 |
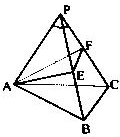 如图,三棱锥P-ABC中,∠APB=∠BPC=∠CPA=30°PA=PB=PC=a,E,F分别为PB,PC上的点,则△AEF周长的最小值等于 ( )
如图,三棱锥P-ABC中,∠APB=∠BPC=∠CPA=30°PA=PB=PC=a,E,F分别为PB,PC上的点,则△AEF周长的最小值等于 ( ) 某厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
某厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )