题目内容
求函数y=
的定义域．
cosx-
|
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数成立的条件即可求函数的定义域．
解答：
解：要使函数有意义，则cosx-
≥0，
即cosx≥
，
则2kπ-
≤x≤2kπ+
，k∈Z，
故函数的定义域为[2kπ-
，2kπ+
]，k∈Z
| 1 |
| 2 |
即cosx≥
| 1 |
| 2 |
则2kπ-
| π |
| 3 |
| π |
| 3 |
故函数的定义域为[2kπ-
| π |
| 3 |
| π |
| 3 |
点评：本题主要考查函数的定义域的求解，要求熟练掌握常见函数成立的条件
练习册系列答案
相关题目
已知向量
，
满足|
-
|=
，
•
=1，则|
+
|=（ ）
| a |
| b |
| a |
| b |
| 6 |
| a |
| b |
| a |
| b |
A、
| ||
B、2
| ||
C、
| ||
| D、10 |
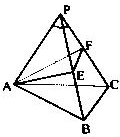如图，三棱锥P-ABC中，∠APB=∠BPC=∠CPA=30°PA=PB=PC=a，E，F分别为PB，PC上的点，则△AEF周长的最小值等于 （ ）