题目内容
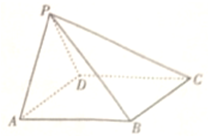 已知四棱锥P-ABCD,侧面PAD⊥底面ABCD,侧面PAD为等边三角形,底面ABCD为棱形且∠DAB=
已知四棱锥P-ABCD,侧面PAD⊥底面ABCD,侧面PAD为等边三角形,底面ABCD为棱形且∠DAB=| π |
| 3 |
(Ⅰ)求证:PB⊥AD;
(Ⅱ)求平面PAB与平面PCD所成的角(锐角)的余弦值.
考点:二面角的平面角及求法,平面与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(Ⅰ)取AD中点O,连结PO,BO,由等边三角形性质得PO⊥AD,由菱形性质得BO⊥AD,从而AD⊥平面POB,由此能证明PB⊥AD.
(Ⅱ)以O为原点,OA为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,设AB=2,求出平面PAB的法向量和平面PCD的法向量,由此利用向量法能求出平面PAB与平面PCD所成的角(锐角)的余弦值.
(Ⅱ)以O为原点,OA为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,设AB=2,求出平面PAB的法向量和平面PCD的法向量,由此利用向量法能求出平面PAB与平面PCD所成的角(锐角)的余弦值.
解答:
(Ⅰ)证明: 取AD上点O,连结PO,BO,
取AD上点O,连结PO,BO,
∵侧面PAD为等边三角形,∴PO⊥AD,
∵底面ABCD为棱形且∠DAB=
,
∴BO⊥AD,又PO∩BO=O,
∴AD⊥平面POB,
又PB?平面POB,∴PB⊥AD.
(Ⅱ)解:∵四棱锥P-ABCD,侧面PAD⊥底面ABCD,
∴PO⊥平面ABCD,又OA⊥OB,
∴以O为原点,OA为x轴,OB为y轴,OP为z轴,
建立空间直角坐标系,设AB=2,
则A(1,0,0),B(0,
,0),P(0,0,
),
C(-2,
,0),D(-1,0,0),
=(1,0,-
),
=(0,
,-
),
设平面PAB的法向量
=(x,y,z),
则
,取y=
,得
=(3,
,
),
=(-2,
,-
),
=(-1,0,-
),
设平面PCD的法向量
=(a,b,c),
则
,取c=
,得
=(-3,-
,
),
设平面PAB与平面PCD所成的角(锐角)为θ,
cosθ=|cos<
,
>|=|
|=|
|=
.
平面PAB与平面PCD所成的角(锐角)的余弦值为
.
 取AD上点O,连结PO,BO,
取AD上点O,连结PO,BO,∵侧面PAD为等边三角形,∴PO⊥AD,
∵底面ABCD为棱形且∠DAB=
| π |
| 3 |
∴BO⊥AD,又PO∩BO=O,
∴AD⊥平面POB,
又PB?平面POB,∴PB⊥AD.
(Ⅱ)解:∵四棱锥P-ABCD,侧面PAD⊥底面ABCD,
∴PO⊥平面ABCD,又OA⊥OB,
∴以O为原点,OA为x轴,OB为y轴,OP为z轴,
建立空间直角坐标系,设AB=2,
则A(1,0,0),B(0,
| 3 |
| 3 |
C(-2,
| 3 |
| PA |
| 3 |
| PB |
| 3 |
| 3 |
设平面PAB的法向量
| n |
则
|
| 3 |
| n |
| 3 |
| 3 |
| PC |
| 3 |
| 3 |
| PD |
| 3 |
设平面PCD的法向量
| m |
则
|
| 3 |
| m |
| 3 |
| 3 |
设平面PAB与平面PCD所成的角(锐角)为θ,
cosθ=|cos<
| m |
| n |
| ||||
|
|
| -9-3+3 | ||||
|
| 3 |
| 5 |
平面PAB与平面PCD所成的角(锐角)的余弦值为
| 3 |
| 5 |
点评:本题主要考查直线与平面、平面与平面之间的平行、垂直等位置关系,考查线线垂直、二面角的概念、求法等知识,考查空间想象能力和逻辑推理能力,是中档题.

练习册系列答案
相关题目
在三棱锥P-ABC中,PA⊥底面ABC,∠APC=∠BPA=30°,∠BAC=120°,PA=3,则三棱锥P-ABC的体积为( )
| A、21π | ||||
| B、12π | ||||
C、
| ||||
D、
|
齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马,现双方各出上、中、下等马各一匹分组分别进行一场比赛,胜两场及以上者获胜,若双方均不知道对方马的出场顺序,则田忌获胜的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f(x)唯一的一个零点同时在区间(2,16),(2,8),(2,4)内,那么下列命题中正确的是( )
| A、f(x)在区间(2,3)内有零点 |
| B、f(x)在区间(2,3)或(3,4)内有零点 |
| C、f(x)在区间(3,16)内无零点 |
| D、f(x)在区间(4,16)内无零点 |
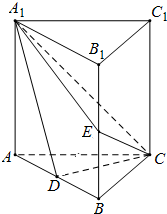 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=