题目内容
在△ABC中,已知
•
=16,sinC=cosAsinB,S△ABC=6,P为线段AC上的点,且
=x
+y
,则xy的最大值为( )
| AB |
| AC |
| BP |
| ||
|
|
| ||
| |BA| |
| A、4 | B、3 | C、2 | D、1 |
考点:平面向量的基本定理及其意义,平面向量数量积的运算
专题:平面向量及应用
分析:在△ABC中,由sinC=cosAsinB,求得cosB=0,可得B=
.由
•
=16 求得|AB|=4,由S△ABC=6,求得|BC|=3.
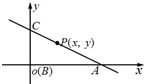
如图以B为原点,BA方向为x轴建立平面直角坐标系,由P为线段AC上的点可设
=λ
(0<λ<1),即(x-4,y)=λ(-4,3),解得x=4-4λ,y=3λ,计算xy的值,并利用基本不等式求得它的最大值.
| π |
| 2 |
| AB |
| AC |
如图以B为原点,BA方向为x轴建立平面直角坐标系,由P为线段AC上的点可设
| AP |
| AC |
解答:
 解:在△ABC中,∵sinC=cosAsinB,可得sinAcosB+cosAsinB=cosAsinB,
解:在△ABC中,∵sinC=cosAsinB,可得sinAcosB+cosAsinB=cosAsinB,
由sinA>0得cosB=0,∴B=
.
由
•
=16 得|
|2=16,∴|AB|=4,由S△ABC=6,求得|BC|=3.
如图以B为原点,BA方向为x轴建立平面直角坐标系,由
=x
+y
及向量坐标的定义,
可知P(x,y),A(4,0),B(0,3),
由P为线段AC上的点可设
=λ
(0<λ<1),即(x-4,y)=λ(-4,3),
得:x=4-4λ,y=3λ,∴xy=3λ(4-4λ)=12λ(1-λ)≤12×(
)2=3.
 解:在△ABC中,∵sinC=cosAsinB,可得sinAcosB+cosAsinB=cosAsinB,
解:在△ABC中,∵sinC=cosAsinB,可得sinAcosB+cosAsinB=cosAsinB,由sinA>0得cosB=0,∴B=
| π |
| 2 |
由
| AB |
| AC |
| AB |
如图以B为原点,BA方向为x轴建立平面直角坐标系,由
| BP |
| ||
|
|
| ||
|
|
可知P(x,y),A(4,0),B(0,3),
由P为线段AC上的点可设
| AP |
| AC |
得:x=4-4λ,y=3λ,∴xy=3λ(4-4λ)=12λ(1-λ)≤12×(
| λ+1-λ |
| 2 |
点评:本题主要考查三角恒等变换,平面向量基本定理及其意义,两个向量坐标形式的运算,属于基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
定义在R上的函数f(x)=
,则f(x)( )
| x+1 | ||
|
| A、既有最大值也有最小值 |
| B、既没有最大值,也没有最小值 |
| C、有最大值,但没有最小值 |
| D、没有最大值,但有最小值 |
下列函数在其定义域上既是奇函数又是减函数的是( )
| A、f(x)=x3 | ||
| B、f(x)=sinx | ||
C、f(x)=
| ||
| D、f(x)=-x|x| |
若指数函数y=(a2-1)x在x∈R上是减函数,则a的取值范围是( )
| A、a>1或a<-1 | ||||
B、-
| ||||
C、a>
| ||||
D、1<a<
|
数列{an}:1,-
,
,-
,…的一个通项公式是( )
| 5 |
| 8 |
| 7 |
| 15 |
| 9 |
| 24 |
A、an=(-1)n+1
| ||
B、an=(-1)n-1
| ||
C、an=(-1)n+1
| ||
D、an=(-1)n-1
|
已知函数f(x)=2x+3,若f(a)=1,则a=( )
| A、-2 | B、-1 | C、1 | D、2 |
对于任意向量
,
,下列命题中正确的是( )
| a |
| b |
A、如果
| ||||||||||||||||
B、|
| ||||||||||||||||
C、|
| ||||||||||||||||
D、|
|
若x∈(0,1),则下列结论正确的是( )
A、lgx>x
| ||
B、2x>x
| ||
C、x
| ||
D、2x>lgx>x
|