题目内容

1．复数z满足z=$\frac{7+i}{1-2i}$（i为虚数单位），则复数z的共轭复数$\overline{z}$=（　　）
A．1+3iB．1-3iC．3-iD．3+i

分析 利用复数代数形式的乘除运算化简，再由共轭复数的概念得答案．

解答 解：∵z=$\frac{7+i}{1-2i}$=$\frac{（7+i）（1+2i）}{（1-2i）（1+2i）}=\frac{5+15i}{5}=1+3i$，
∴$\overline{z}=1-3i$．
故选：B．

点评 本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础题．

练习册系列答案
相关题目
13．已知集合A={-1，0}，B={x|-1＜x＜1}，则A∩B=（　　）
A．{-1}B．{0}C．{-1，0}D．{-1，0，1}
12．观察下列各式：1=12，2+3+4=32，3+4+5+6=52，4+5+6+7+8+9+10=72，…，可以得出的一般结论是（　　）
A．n+（n+1）+（n+2）+…+（3n-2）=n2B．n+（n+1）+（n+2）+…+（3n-2）=（2n-1）2
C．n+（n+1）+（n+2）+…+（3n-1）=n2D．n+（n+1）+（n+2）+…+（3n-1）=（2n-1）2
9．在直角坐标系xOy中，曲线C1的参数方程为$\left\{\begin{array}{l}x=-t\\ y=\sqrt{3}t\end{array}\right.$（t为参数，-1≤t≤1），当t=1时，曲线C1上的点为A，当t=-1时，曲线C1上的点为B，以O为极点，x轴的正半轴为极轴建立极坐标系．曲线C2的极坐标方程$ρ=\frac{6}{{\sqrt{4+5{{sin}^2}θ}}}$
（Ⅰ） 求线段AB的极坐标方程；C2的参数方程
（Ⅱ） 设M是曲线C2上的动点，求|MA|2+|MB|2最大值及取最大值时点M的直角坐标．
16．某几何体的三视图如图所示，则该几何体的体积为（　　）
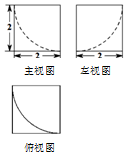
A．$8-\frac{4}{3}π$B．$8-\frac{8}{3}π$C．24-πD．24+π
6．已知$a=\frac{1}{b}＞1$，如果方程ax=logbx，bx=logax，bx=logbx的根分别为x1，x2，x3，则x1，x2，x3的大小关系为（　　）
A．x3＜x1＜x2B．x3＜x2＜x1C．x1＜x3＜x2D．x1＜x2＜x3
13．已知函数f（x）=4x3+ax2+bx+5在x=-1与x=$\frac{3}{2}$处有极值，则函数的单调递减区间为（-1，$\frac{3}{2}$）．
10．已知数列{an}中，a3=2，a7=1，若数列$\left\{{\frac{1}{{1+{a_n}}}}\right\}$是等差数列，则a11等于（　　）
A．0B．$\frac{1}{3}$C．$\frac{1}{6}$D．$\frac{1}{2}$
11．已知x+y+z=1．
证明：（1）x2+y2+z2≥xy+yz+zx，
（2）x2+y2+z2≥$\frac{1}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网