题目内容
已知sin(x+
)=
，sin(x-
)=
，则tanx= ．
| π |
| 4 |
| 3 |
| 5 |
| π |
| 4 |
| 4 |
| 5 |
考点：两角和与差的正切函数,两角和与差的正弦函数
专题：三角函数的求值
分析：利用两角和和差的正弦公式，展开进行整理即可得到结论．
解答：
解：∵sin(x+
)=
，sin(x-
)=
，
∴
，
两式相比得
=
，
即4sinx+4cosx=3sinx-3cosx，
∴sinx=-7cosx，
∴tanx=-7，
故答案为：-7
| π |
| 4 |
| 3 |
| 5 |
| π |
| 4 |
| 4 |
| 5 |
∴
|
两式相比得
| sin?x+cos?x |
| sin?x-cos?x |
| 3 |
| 4 |
即4sinx+4cosx=3sinx-3cosx，
∴sinx=-7cosx，
∴tanx=-7，
故答案为：-7
点评：本题主要考查两角和差的正弦公式的应用，要求熟练掌握相应的三角公式．
练习册系列答案
相关题目
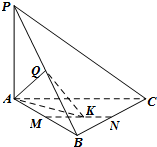如图，在三棱锥P-ABC中，直线PA⊥平面ABC，且∠ABC=90°，又点Q，M，N分别是线段PB，AB，BC的中点，且点K是线段MN上的动点．
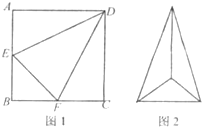如图1，边长为2的d正方形ABCD中，E，F 分别是AB，BC的中点，将△ADE，△CDF，△BEF折起，使A，C，B二点重合于G，所得二棱锥G-DEF的俯视图如图2，则其正视图的面积为如图是一个体积为10的空间几何体的三视图，则图中x的值为（ ）
| A、2 | B、3 | C、4 | D、5 |