题目内容
已知函数f（x）=e|x|，m＞1，对任意的x∈（1，m），都有f（x-2）≤ex，则最大的正整数m为 ．
考点：指数函数的图像与性质
专题：函数的性质及应用
分析：在同一坐标系中作出y1=f（x-2）和y2=ex的图象，结合图形分析得出当x=4时，y1=e2＜y2=4e，当x=5时，y1=e3＞y2=5e，从而得出结论．
解答：
解：∵f（x）=e|x|，
∴f（x-2）=）=e|x-2|，
在同一坐标系中作出y1=e|x-2|和y2=ex的图象，如图所示：
由图知：当x=1时，y1=y2，
当x=4时，y1=e2＜y2=4e，
当x=5时，y1=e3＞y2=5e，
∴m＜5；
∴最大的正整数m为4；
故答案为：4．
∴f（x-2）=）=e|x-2|，
在同一坐标系中作出y1=e|x-2|和y2=ex的图象，如图所示：
由图知：当x=1时，y1=y2，
当x=4时，y1=e2＜y2=4e，
当x=5时，y1=e3＞y2=5e，
∴m＜5；
∴最大的正整数m为4；
故答案为：4．
点评：本题考查了指数函数的图象与性质以及数形结合的思想，在同一坐标系中画出两个函数的图象是解题的关键．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
在△ABC中，∠BAC=120°，AB=
如图是一个几何体的三视图，若它的体积为2，则a+b的最小值为
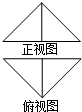把边长为