题目内容
由方程2x|x|-y=1所确定的x,y的函数关系记为y=f(x),给出如下结论:
(1)f(x)是R上的单调递增函数;
(2)f(x)的图象关于直线x=0对称;
(3)对于任意x∈R,f(x)+f(-x)=-2恒成立.
其中正确的结论为 (写出所有正确结论的序号).
(1)f(x)是R上的单调递增函数;
(2)f(x)的图象关于直线x=0对称;
(3)对于任意x∈R,f(x)+f(-x)=-2恒成立.
其中正确的结论为
考点:函数解析式的求解及常用方法
专题:数形结合,函数的性质及应用
分析:由方程2x|x|-y=1所确定的x,y的函数关系记为y=f(x),f(x)=2x|x|-1═
,
,分别画出当x≥0和x<0的函数图象,它们分别是抛物线的一部分.如图所示.结合观察图象可得答案.
|
,分别画出当x≥0和x<0的函数图象,它们分别是抛物线的一部分.如图所示.结合观察图象可得答案.
解答:
 解:由方程2x|x|-y=1所确定的x,y的函数关系记为y=f(x),
解:由方程2x|x|-y=1所确定的x,y的函数关系记为y=f(x),
则f(x)=2x|x|-1=
,
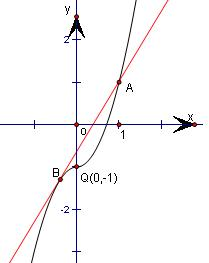
分别画出当x≥0和x<0的函数图象,它们分别是抛物线的一部分.如图所示.
观察图象可知:
(1)f(x)是R上的单调递增函数; 正确;
(2)图象不关于x=0对称,(2)错误;
(3)图象关于点Q(0,-1)对称,故对于任意x∈R,f(x)+f(-x)=-2恒成立;正确;
故答案为:(1)(3).
 解:由方程2x|x|-y=1所确定的x,y的函数关系记为y=f(x),
解:由方程2x|x|-y=1所确定的x,y的函数关系记为y=f(x),则f(x)=2x|x|-1=
|
分别画出当x≥0和x<0的函数图象,它们分别是抛物线的一部分.如图所示.
观察图象可知:
(1)f(x)是R上的单调递增函数; 正确;
(2)图象不关于x=0对称,(2)错误;
(3)图象关于点Q(0,-1)对称,故对于任意x∈R,f(x)+f(-x)=-2恒成立;正确;
故答案为:(1)(3).
点评:本小题主要考查分段函数、函数单调性的应用、函数对称性的应用、带绝对值的函数等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
数列{an}的通项式an=
,则数列{an}中的最大项是( )
| n |
| n2+90 |
| A、第9项 |
| B、第10项和第9项 |
| C、第10项 |
| D、第9项和第8项 |
在△ABC中,若a2=bc,则角A为( )
| A、锐角 | B、钝角 | C、直角 | D、60° |
 如图,山脚下有一小塔AB,在塔底B测得山顶C的仰角为60°,在山顶C测得塔顶A的俯角为45°,已知塔高AB=20m,求山高CD.
如图,山脚下有一小塔AB,在塔底B测得山顶C的仰角为60°,在山顶C测得塔顶A的俯角为45°,已知塔高AB=20m,求山高CD.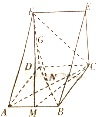 已知直三棱柱BCE-ADG,底面△ADF中,AD⊥DF,DA=DF=DC,其中M,N分别是AB,AC的中点,G是DF上的一个动点.
已知直三棱柱BCE-ADG,底面△ADF中,AD⊥DF,DA=DF=DC,其中M,N分别是AB,AC的中点,G是DF上的一个动点.