题目内容
4.已知定义在R上的奇函数f(x)满足f(x-4)=-f(x),且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4=-8.分析 由条件“f(x-4)=-f(x)”得f(x+8)=f(x),说明此函数是周期函数,又是奇函数,且在[0,2]上为增函数,由这些画出示意图,由图可解决问题.
解答 解:∵f(x)是奇函数,
∴f(x-4)=-f(x)=f(-x),
∴f(x)的图象关于直线x=-2对称,
又f(x-4)=-f(x),∴f(x)=-f(x+4),
∴f(x-4)=f(x+4),∴f(x)周期为8,
作出f(x)的大致函数图象如图: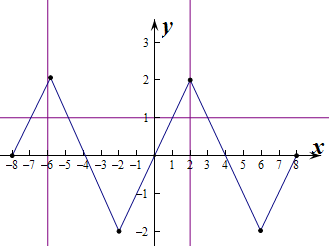
由图象可知f(x)=m的4个根中,两个关于直线x=-6对称,两个关于直线x=2对称,
∴x1+x2+x3+x4=-6×2+2×2=-8.
故答案为:-8.
点评 本题主要考查方程根的应用,根据条件结合函数的周期性和奇偶性,利用数形结合是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知O是三角形ABC所在平面内一点,且满足$\overrightarrow{BA}$•$\overrightarrow{OA}$+$\overrightarrow{BC}$2=$\overrightarrow{AB}$•$\overrightarrow{OB}$+$\overrightarrow{AC}$2,则点O在( )
| A. | AB边中线所在的直线上 | B. | ∠C平分线所在的直线上 | ||
| C. | 与AB垂直的直线上 | D. | 三角形ABC的外心 |
9.执行如下框图所示算法,若实数a、b不相等,依次输入a+b,a,b,输出值依次记为f(a+b),f(a),f(b),则f(a+b)-f(a)-f(b)的值为( )

| A. | 0 | B. | 1或-1 | C. | 0或±1 | D. | 以上均不正确 |
11.设l、m是两条不同的直线,α是一个平面,则下列说法正确的是( )
| A. | 若l⊥m,m⊆α则l⊥α | B. | 若l∥α,m⊆α则l∥m | C. | 若l⊥α,l∥m则m⊥α | D. | 若l∥α,m∥α则l∥m |
9.若函数f(x)=sinωx+cosωx(ω>0)的图象相邻的两条对称轴的距离为$\frac{π}{3}$,则ω的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{π}$ | C. | 3 | D. | 6 |