题目内容
9.若函数f(x)=sinωx+cosωx(ω>0)的图象相邻的两条对称轴的距离为$\frac{π}{3}$,则ω的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{3}{π}$ | C. | 3 | D. | 6 |
分析 利用两角和的正弦公式化简函数的解析式,再结合题意利用正弦函数的图象的对称性求得ω的值.
解答 解:∵函数f(x)=sinωx+cosωx=$\sqrt{2}$sin(ωx+$\frac{π}{4}$)(ω>0)的图象相邻两条对称轴之间的距离为$\frac{π}{ω}=\frac{π}{3}$,
∴ω=3.
故选:C.
点评 本题主要考查两角和的正弦公式,正弦函数的图象的对称性,属于基础题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
2.直线l1:Ax+By+C1=0关于直线l2:Ax+By+C2=0(C1≠C2)对称的直线方程是( )
| A. | Ax+By+(C1-2C2)=0 | B. | Ax+By+(C2-2C1)=0 | C. | Ax+By+(2C2-C1)=0 | D. | Ax+By+(2C1-C2)=0 |
4.已知集合A={x|(x+2)(x-3)≤0,x∈Z},B={x|(x+1)(x-1)(x-3)=0},则A∩B=( )
| A. | {-1,1} | B. | {1,3} | C. | {-1,1,3} | D. | {-3,-1,1} |
15.执行右面的程序框图,如果输出的a值大于2017,那么判断框内的条件为( )

| A. | k<9? | B. | k≥9? | C. | k<10? | D. | k≥11? |
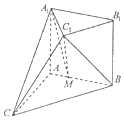 如图,在多面体ABCA1B1C1中,四边形ABB1A1是正方形,CA⊥平面ABB1A1,AC=AB=1,B1C1∥BC,BC=2B1C1.
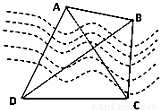
如图,在多面体ABCA1B1C1中,四边形ABB1A1是正方形,CA⊥平面ABB1A1,AC=AB=1,B1C1∥BC,BC=2B1C1.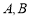 两点都在河的对岸(不可到达),为了测量
两点都在河的对岸(不可到达),为了测量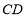 ,测得:
,测得: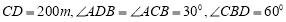 ,则
,则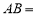 ()
()
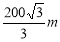 B.
B.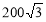
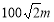 D.数据不够,无法计算
D.数据不够,无法计算