题目内容
下列函数中，既是奇函数又是增函数的为（ ）
| A、y=x+1 | ||
| B、y=-x3 | ||
C、y=
| ||
| D、y=x|x| |
考点：函数单调性的判断与证明,函数奇偶性的判断
专题：函数的性质及应用
分析：根据奇函数的定义，导数符号和函数单调性的关系，反比例函数的单调性，二次函数的单调性即可找出正确选项．
解答：
解：A．该函数不是奇函数，所以该选项错误；
B．y′=-3x2≤0，所以该函数是减函数，所以该选项错误；
C．该函数是反比例函数，该函数在（-∞，0），（0，+∞）单调递增，所以在定义域{x|x=0}上不具有单调性，所以该选项错误；
D．容易判断该函数是奇函数，y=
，根据二次函数的单调性x2在[0，+∞）是增函数，-x2在（-∞，0）上是增函数，所以函数y在R上是增函数，所以该选项正确．
故选D．
B．y′=-3x2≤0，所以该函数是减函数，所以该选项错误；
C．该函数是反比例函数，该函数在（-∞，0），（0，+∞）单调递增，所以在定义域{x|x=0}上不具有单调性，所以该选项错误；
D．容易判断该函数是奇函数，y=
|
故选D．
点评：考查奇函数的定义，y=-x3的单调性，反比例函数的单调性，分段函数的单调性，以及二次函数的单调性．
练习册系列答案
阅读快车系列答案
相关题目
已知复数z1=1-i，z2=1+i，则
等于（ ）
| z1-z2 |
| i |
| A、2i | B、-2 |
| C、2+i | D、-2+i |
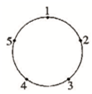如图，圆周上按顺时针方向标有1，2，3，4，5五个点，一只青蛙按顺时针方向绕圆从一个点跳到另一点；若停在奇数点上，则下一次只能跳一个点；若停在偶数点上，则下一次可以跳两个点，该青蛙从5这点跳起，跳2008次后它将停在的点是（ ）| A、1 | B、2 | C、3 | D、4 |
集合P={（x，y）|y=k}，Q={（x，y）|y=ax+1，a＞0，a≠1}，已知P∩Q只有一个子集，那么实数k的取值范围是（ ）
| A、（-∞，1） |
| B、（-∞，1] |
| C、（1，+∞） |
| D、（-∞，+∞） |
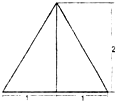一个三棱锥的侧棱长都相等，底面是正三角形，其正（主）视图如右图所示．该三棱锥侧面积和体积分别是（ ）A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、8，
|
在△ABC中，根据下列条件解三角形，其中有两个解的是（ ）
| A、b=10，A=45°，C=60° |
| B、a=6，c=5，B=60° |
| C、a=7，b=5，A=60° |
| D、a=14，b=16，A=45° |
在数列{an}，a1=1，an+1=
（n∈N*），则a5=（ ）
| 2an |
| an+2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设f0（x）=cosx，且对任意的n∈N，都有 fn+1（x）=fn′（x），则f2013（x）=（ ）
| A、cosx | B、sinx |
| C、-sinx | D、-cosx |