题目内容
下列命题正确的个数是( )
①“在三角形ABC中,若sinA>sinB,则A>B”的否命题是真命题;
②命题p:x≠2或y≠3,命题q:x+y≠5则p是q的必要不充分条件;
③“?x∈R,x3-x2+1≤0”的否定是“?x∈R,x3-x2+1>0”.
①“在三角形ABC中,若sinA>sinB,则A>B”的否命题是真命题;
②命题p:x≠2或y≠3,命题q:x+y≠5则p是q的必要不充分条件;
③“?x∈R,x3-x2+1≤0”的否定是“?x∈R,x3-x2+1>0”.
| A、0 | B、1 | C、2 | D、3 |
考点:四种命题,命题的否定
专题:简易逻辑
分析:①先写出该命题的否命题:在三角形ABC中,若sinA≤sinB,则A≤B,所以分这样几种情况判断即可:A,B∈(0,
],A∈(0,
],B∈(
,π),A∈(
,π),B∈(0,
];
②根据必要不充分条件的概念即可判断该命题是否正确;
③根据全称命题的否定是特称命题即可判断该命题是否正确.
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
②根据必要不充分条件的概念即可判断该命题是否正确;
③根据全称命题的否定是特称命题即可判断该命题是否正确.
解答:
解:①该命题的否命题是:在三角形ABC中,若sinA≤sinB,则A≤B;
若A,B∈(0,
],∵正弦函数y=sinx在(0,
]上是增函数,∴sinA≤sinB可得到A≤B;
若A∈(0,
],B∈(
,π),sinA<sinB能得到A<B;
若A∈(
,π),B∈(0,
],则由sinA≤sinB,得到sin(π-A)≤sinB,∴π≤A+B,显然这种情况不存在;
综上可得sinA≤sinB能得到A≤B,所以该命题正确;
②由x≠2,或y≠3,得不到x+y≠5,比如x=1,y=4,x+y=5,∴p不是q的充分条件;
若x+y≠5,则一定有x≠2且y≠3,即能得到x≠2,或y≠3,∴p是q的必要条件;
∴p是q的必要不充分条件,所以该命题正确;
③根据全称命题的否定是特称命题知道该命题正确;
所以命题正确的个数为3.
故选:D.
若A,B∈(0,
| π |
| 2 |
| π |
| 2 |
若A∈(0,
| π |
| 2 |
| π |
| 2 |
若A∈(
| π |
| 2 |
| π |
| 2 |
综上可得sinA≤sinB能得到A≤B,所以该命题正确;
②由x≠2,或y≠3,得不到x+y≠5,比如x=1,y=4,x+y=5,∴p不是q的充分条件;
若x+y≠5,则一定有x≠2且y≠3,即能得到x≠2,或y≠3,∴p是q的必要条件;
∴p是q的必要不充分条件,所以该命题正确;
③根据全称命题的否定是特称命题知道该命题正确;
所以命题正确的个数为3.
故选:D.
点评:考查正弦函数的单调性,充分条件、必要条件、必要不充分条件的概念,特称命题与全称命题的关系.

练习册系列答案
相关题目
在△ABC中,已知a=6,b=8,A=30°,则sinB=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
“|x-A|<
,且|y-A|<
”是“|x-y|<?”(x,y,A,?∈R)的( )
| ? |
| 2 |
| ? |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知集合A={x|x2-2x>0},B={x|-2<x<
},则( )
| 6 |
| A、A∩B=∅ | B、A∪B=R |
| C、B⊆A | D、A⊆B |
下列函数中,既是奇函数又是增函数的为( )
| A、y=x+1 | ||
| B、y=-x3 | ||
C、y=
| ||
| D、y=x|x| |
在如图程序框图的结构中最突出的逻辑结构及输出的i的值是( )
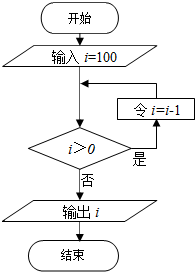

| A、当型循环结构,-1 |
| B、直到型循环结构,-1 |
| C、当型循环结构,0 |
| D、直到型循环结构,0 |
已知函数f(x)是定义在R上的奇函数,f(1)=0,当x>0时,有
>0成立,则不等式f(x)>0的解集是( )
| xf′(x)-f(x) |
| x2 |
| A、(-1,0)∪(1,+∞) |
| B、(-1,0) |
| C、(1,+∞) |
| D、(-∞,-1)∪(1,+∞) |
已经集合M={-1,0,1,2,3,4,5},N={x|x≤1或x≥4},则M∩N=( )
| A、{-1,0,1,4,5} |
| B、{1,2,3,4} |
| C、{-1,0,5} |
| D、{-1,0,1,5} |
已知函数f(x)是R上的增函数,A(0,-2),B(4,2)是其图象上的两点,那么|f(
)|<2的解集是( )
| 1 |
| 2x+1 |
| A、(1,4) |
| B、(1,+∞) |
| C、(-∞,1)∪[4,+∞] |
| D、(-3,+∞) |