题目内容
若“*“表示一种运算,满足如下关系,(1)1*1=2,(2)(n+1)*1=3(n*1)+2 (n∈N*) 则n*1= .
考点:函数的值
专题:函数的性质及应用
分析:由已知得1*1=2=31-1,2*1=3×2+2=8=32-1,3*1=3×8+2=26=33-1,4*1=3×26+2=80=34-1,…,由此猜想出n*1的表达式.
解答:
解:∵1*1=2,(n+1)*1=3(n*1)+2 (n∈N*),
∴1*1=2=31-1,
2*1=3×2+2=8=32-1,
3*1=3×8+2=26=33-1,
4*1=3×26+2=80=34-1,
…
由此猜想:n*1=3n-1.
故答案为:3n-1.
∴1*1=2=31-1,
2*1=3×2+2=8=32-1,
3*1=3×8+2=26=33-1,
4*1=3×26+2=80=34-1,
…
由此猜想:n*1=3n-1.
故答案为:3n-1.
点评:本题考查函数的表达式的求法,是基础题,解题时要注意寻找规律,进行合理猜想.

练习册系列答案
相关题目
下列有关命题的说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” |
| B、命题“若x=y,则sinx=siny”的逆否命题为真命题 |
| C、若p∧q为假命题,则p,q均为假命题 |
| D、若关于x的不等式ax2+ax-2<0恒成立,则-8<a<0 |
设tanα、tanβ是方程x2+x-2=0的两实数根,则tan(α+β)的值为( )
| A、-1 | ||
B、-
| ||
C、
| ||
| D、1 |
已知α是第二象限角,P(x,
)为其终边上一点,且cosα=
x,则x=( )
| 5 |
| ||
| 4 |
A、
| ||
B、±
| ||
C、-
| ||
D、-
|
 如图,某商业中心O有通往正东方向和北偏东30°方向的两条街道,某公园P位于商业中心北偏东θ角(0<θ<
如图,某商业中心O有通往正东方向和北偏东30°方向的两条街道,某公园P位于商业中心北偏东θ角(0<θ<
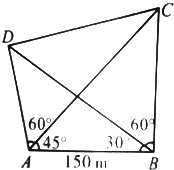 如图,A、B、C、D是河两岸的四根电线杆,A、B在河这边,C、D在河对岸,现在距离A处150m的B处测得∠ABD=30°,∠DBC=60°,而在A处测得∠BAC=45°,∠CAD=60°,求C、D两点间的距离.(已知A、B、C、D在同一平面内).
如图,A、B、C、D是河两岸的四根电线杆,A、B在河这边,C、D在河对岸,现在距离A处150m的B处测得∠ABD=30°,∠DBC=60°,而在A处测得∠BAC=45°,∠CAD=60°,求C、D两点间的距离.(已知A、B、C、D在同一平面内). 已知AB是圆O的直径,P是上半圆上的任意一点,PC是∠APB的平分线,E是下半圆的中点.
已知AB是圆O的直径,P是上半圆上的任意一点,PC是∠APB的平分线,E是下半圆的中点.