Question

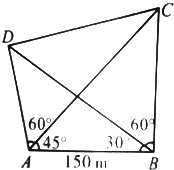如图，A、B、C、D是河两岸的四根电线杆，A、B在河这边，C、D在河对岸，现在距离A处150m的B处测得∠ABD=30°，∠DBC=60°，而在A处测得∠BAC=45°，∠CAD=60°，求C、D两点间的距离．（已知A、B、C、D在同一平面内）．

Answer 1

考点：解三角形的实际应用

专题：综合题,解三角形

分析：根据题中条件，在△ADB中由正弦定理求得DB，在△DBC中由余弦定理求得DC．

解答： 解：如图可知∠ABC=90°
∵∠BAC=45°，∴∠BCA=45°
∴AB=CB=150m
∵∠BAC=45°，∠CAD=60°，∠ABD=30°，
∴∠ADB=45°，
∴

150

2 2

=

DB

6 + 2 4

，
∴DB=75（

3

+1）
∴CD=

1502+[75( 3 +1)]2-2×150×75( 3 +1)× 1 2

=15

150

m．

点评：本题主要考查正弦定理和余弦定理在实际中的应用．由于图形中三角形比较多，应分清在哪个三角形中利用正弦定理和余弦定理．