题目内容
(文)设x、y均是实数,i是虚数单位,复数(x-2y)+(5-2x-y)i的实部大于0,虚部不小于0,则复数z=x+yi在复平面上的点集用阴影表示为图中的( )
A、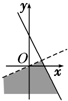 |
B、 |
C、 |
D、 |
考点:复数的代数表示法及其几何意义
专题:数系的扩充和复数
分析:由复数(x-2y)+(5-2x-y)i的实部大于0,虚部不小于0,可得
,利用线性规划的知识可得可行域即可.
|
解答:
解:∵复数(x-2y)+(5-2x-y)i的实部大于0,虚部不小于0,
∴
,
由线性规划的知识可得:可行域为直线x=2y的右下方和直线的左下方,因此为A.
故选:A.
∴
|
由线性规划的知识可得:可行域为直线x=2y的右下方和直线的左下方,因此为A.
故选:A.
点评:本题考查了复数的几何意义和线性规划的可行域,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
已知数列{an}的前n项和Sn=n2-1,则( )
| A、an=2n-1 | |||||
| B、an=2n+1 | |||||
C、an=
| |||||
D、an=
|
已知数列{an}满足:a1=2,且an=1-
(n>1,n∈N+),则a2014的值为( )
| 1 |
| an-1 |
A、
| ||
| B、2 | ||
| C、-1 | ||
| D、1 |
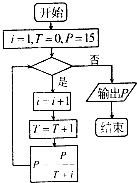 一个算法的程序框图如图所示,若该程序输出的P位于区间(10-4,10-3)内,则判断框内应填入的条件是( )
一个算法的程序框图如图所示,若该程序输出的P位于区间(10-4,10-3)内,则判断框内应填入的条件是( )| A、T≤3 | B、T≤4 |
| C、T≤5 | D、T≤6 |
若抛物线y2=2px(p>0)过点A(8,-8),则点A与抛物线焦点F的距离为( )
| A、9 | ||
| B、10 | ||
| C、12 | ||
D、4
|
执行如图的程序框图,若输出的S是255,则判断框内应填写( )


| A、n≤6? | B、n≤7? |
| C、n≥7? | D、n≥8? |
阅读如图所示程序框图,运行相应程序,则输出的S值为( )


A、-
| ||
B、
| ||
C、
| ||
D、
|
2014年西安地区特长生考试有8所名校招生,若某3位同学恰好被其中的2所名校录取,则不同的录取方法有( )
| A、68种 | B、84种 |
| C、168种 | D、224种 |