题目内容
已知圆C经过A（3，2）、B（1，6）两点，且圆心在直线y=2x上，求圆C的方程．
考点：圆的标准方程
专题：直线与圆
分析：设圆心C（a，2a），由题意得（a-3）2+（2a-2）2=（a-1）2+（2a-6）2，由此能求出圆C的方程．
解答：
解：设圆心C（a，2a），
由题意得（a-3）2+（2a-2）2=（a-1）2+（2a-6）2，
解得a=2，∴C（2，4），
∴r2=（2-3）2+（2×2-2）2=5，
∴圆C的方程为：（x-2）2+（y-4）2=5．
由题意得（a-3）2+（2a-2）2=（a-1）2+（2a-6）2，
解得a=2，∴C（2，4），
∴r2=（2-3）2+（2×2-2）2=5，
∴圆C的方程为：（x-2）2+（y-4）2=5．
点评：本题考查圆的方程的求法，解题时要认真审题，是基础题．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
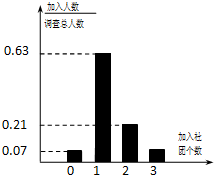为了丰富学校课余文化生活，锻炼学生的综合能力，浏阳一中成立了多个学生社团，并鼓励学生参加社团活动或加入社团组织经过调研，若学生人均加入社团1～2个，则说明社团活动开展得有序．为此，学校规定学生加入的社团个数不能超过3个．社团文化节期间，校团委为了了解学生社团活动开展情况，随机发放并回收了100份调查问卷，并对各项指标进行了统计，其中学生参加社团的个数情况统计如图所示．
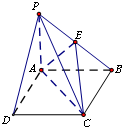在四棱锥P-ABCD中，底面ABCD为边长为4的正方形，PA⊥平面ABCD，E为PB中点，PB=4
如图：（1）将程序框图表示的函数写出来；