题目内容
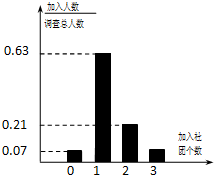 为了丰富学校课余文化生活,锻炼学生的综合能力,浏阳一中成立了多个学生社团,并鼓励学生参加社团活动或加入社团组织经过调研,若学生人均加入社团1~2个,则说明社团活动开展得有序.为此,学校规定学生加入的社团个数不能超过3个.社团文化节期间,校团委为了了解学生社团活动开展情况,随机发放并回收了100份调查问卷,并对各项指标进行了统计,其中学生参加社团的个数情况统计如图所示.
为了丰富学校课余文化生活,锻炼学生的综合能力,浏阳一中成立了多个学生社团,并鼓励学生参加社团活动或加入社团组织经过调研,若学生人均加入社团1~2个,则说明社团活动开展得有序.为此,学校规定学生加入的社团个数不能超过3个.社团文化节期间,校团委为了了解学生社团活动开展情况,随机发放并回收了100份调查问卷,并对各项指标进行了统计,其中学生参加社团的个数情况统计如图所示.(1)求参加调查的100名学生中加入了3个社团的人数;
(2)根据问卷调查统计情况,判断社团活动开展是否有序,并说明理由;
(3)问卷显示没有参加社团的7名同学中有三名男同学,四名女同学,若从这7名同学中随机选两名同学参加座谈,求恰好两名同学都是男同学的概率.
考点:频率分布直方图,古典概型及其概率计算公式
专题:概率与统计
分析:(1)利用频率分布直方图求出加入了3个社团的频率,再求对应的频数;
(2)求出该样本中人均加入社团的个数,由此估计总体平均数,从而判断是否符合社团活动开展有序的标准;
(3)用列举法求出基本事件数,从而求出对应的概率是多少.
(2)求出该样本中人均加入社团的个数,由此估计总体平均数,从而判断是否符合社团活动开展有序的标准;
(3)用列举法求出基本事件数,从而求出对应的概率是多少.
解答:
解:(1)加入了3个社团的人数是
100×(1-0.07-0.63-0.21)=9;
(2)该样本中人均加入社团的个数为:
0.07×0+0.63×1+0.21×2+0.09×3=1.32,
以该样本估计总体平均数为1.32,符合人均加入社团1~2个的指标要求,说明社团活动开展有序;
(3)设三名男同学分别为A、B、C,四名女同学分别为a、b、c、d,
则随机选出两名学生,所有的基本事件如下:
{A,B},{A,C},{B,C},{a,b},{a,c},{a,d},{b,c},{b,d},{c,d},
{A,a},{A,b},{A,c},{A,d},{B,a,},{B,b},{B,c},{B,d},
{C,a},{C,b},{C,c},{C,d}共21个,
恰好两名同学都是男同学包含的基本事件为{A,B},{A,C},{B,C}共3个,
∴恰好两名同学都是男同学的概率是
=
.
100×(1-0.07-0.63-0.21)=9;
(2)该样本中人均加入社团的个数为:
0.07×0+0.63×1+0.21×2+0.09×3=1.32,
以该样本估计总体平均数为1.32,符合人均加入社团1~2个的指标要求,说明社团活动开展有序;
(3)设三名男同学分别为A、B、C,四名女同学分别为a、b、c、d,
则随机选出两名学生,所有的基本事件如下:
{A,B},{A,C},{B,C},{a,b},{a,c},{a,d},{b,c},{b,d},{c,d},
{A,a},{A,b},{A,c},{A,d},{B,a,},{B,b},{B,c},{B,d},
{C,a},{C,b},{C,c},{C,d}共21个,
恰好两名同学都是男同学包含的基本事件为{A,B},{A,C},{B,C}共3个,
∴恰好两名同学都是男同学的概率是
| 3 |
| 21 |
| 1 |
| 7 |
点评:本题考查了频率分布直方图的应用问题,解题时应根据频率分布直方图以及概率的知识进行解答,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=cosπx的图象与函数y=(
)|x-1|(-3≤x≤5)的图象所有交点的横坐标之和等于( )
| 1 |
| 2 |
| A、4 | B、6 | C、8 | D、10 |
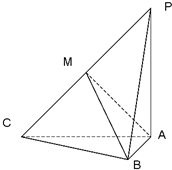 如图,三棱锥P-ABC中,
如图,三棱锥P-ABC中,