题目内容
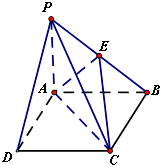 在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点,PB=4
在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点,PB=4| 2 |
(Ⅰ)求证:平面APD⊥平面APB
(Ⅱ)求三棱锥D-AEC的体积.
考点:平面与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(Ⅰ)由线面垂直得PA⊥BA,由正方形性质得DA⊥BA,由此能证明平面PAD⊥平面PAB.
(Ⅱ)由勾股定理求出PA=4,取AB中点F,得EF⊥平面ABCD,且EF=2,由此能求出三棱锥D-AEC的体积.
(Ⅱ)由勾股定理求出PA=4,取AB中点F,得EF⊥平面ABCD,且EF=2,由此能求出三棱锥D-AEC的体积.
解答:
(Ⅰ)证明:AP⊥平面ABCD,
且AB?平面ABCD,∴PA⊥BA,
又∵底面ABCD为正方形,∴DA⊥BA,
又PA∩DA=A,PA,DA?平面PAD,
∴BA⊥平面PAD,又∵AB?平面PAB,
∴平面PAD⊥平面PAB.…(6分)
(Ⅱ)解:由(Ⅰ)知PB2=PA2+AB2,
∵AB=4,PB=4
,∴PA=4,
取AB中点F,则EF∥PA,
∴EF⊥平面ABCD,且EF=2
∴VD-AEC=VE-ADC=
S△ADC•EF=
×
×4×4×2=
.…(13分)
且AB?平面ABCD,∴PA⊥BA,
又∵底面ABCD为正方形,∴DA⊥BA,
又PA∩DA=A,PA,DA?平面PAD,
∴BA⊥平面PAD,又∵AB?平面PAB,
∴平面PAD⊥平面PAB.…(6分)
(Ⅱ)解:由(Ⅰ)知PB2=PA2+AB2,
∵AB=4,PB=4
| 2 |
取AB中点F,则EF∥PA,
∴EF⊥平面ABCD,且EF=2
∴VD-AEC=VE-ADC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 16 |
| 3 |
点评:本题考查平面与平面垂直的证明,考查三棱锥体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知△ABC中,A、B、C的对边分别为a、b、c,若A=30°,C=105°,b=8,则a等于( )
| A、4 | ||
B、4
| ||
C、4
| ||
D、4
|