题目内容
已知函数f(x)=sin(
+
)cos(
-
)-sin2
,先将f(x)的图象向右平移
个单位,再将所得图象上的所有点的横坐标缩短到原来的
,纵坐标伸长到原来的
倍,得到g(x)的图象.
(1)求f(x)的最小正周期;
(2)若x∈[0,
],求f(x)的值域;
(3)若F(x)=2af(x)+
g(x)+1,x∈[0,
],a≠0,试求F(x)的最小值.
| x |
| 2 |
| π |
| 4 |
| x |
| 2 |
| π |
| 4 |
| x |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| 2 |
(1)求f(x)的最小正周期;
(2)若x∈[0,
| π |
| 4 |
(3)若F(x)=2af(x)+
| a |
| 2 |
| π |
| 4 |
考点:函数y=Asin(ωx+φ)的图象变换,三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:(1)利用三角恒等变换化简函数的解析式为f(x)=
sin(x+
),从而求得它的周期.
(2)由条件利用正弦函数的定义域和值域求得f(x)的值域.
(3)由条件利用函数y=Asin(ωx+φ)的图象变换规律,求得g(x)=sin2x,再利用三角恒等变换求得F(x)=a(sinx+cosx+sinxcosx),令sinx+cosx=t,可得F(x)=
(t+1)2+1-a,分类讨论结合t的范围以及二次函数的性质,求得F(x)的最小值.
| ||
| 2 |
| π |
| 4 |
(2)由条件利用正弦函数的定义域和值域求得f(x)的值域.
(3)由条件利用函数y=Asin(ωx+φ)的图象变换规律,求得g(x)=sin2x,再利用三角恒等变换求得F(x)=a(sinx+cosx+sinxcosx),令sinx+cosx=t,可得F(x)=
| a |
| 2 |
解答:
解:(1)∵函数f(x)=sin(
+
)cos(
-
)-sin2
=cos(
-
)cos(
-
)-sin2
=
-
=
(sinx+cosx)=
sin(x+
),
∴函数f(x)的周期为
=2π.
(2)∵x∈[0,
],∴x+
∈[
,
],∴sin(x+
)∈[
,1],
∴f(x)∈[
,
].
(3)将f(x)的图象向右平移
个单位,再将所得图象上的所有点的横坐标缩短到原来的
,
纵坐标伸长到原来的
倍,得到g(x)=sin2x的图象,
F(x)=2af(x)+
g(x)+1=
asin(x+
)+
sin2x=a(sinx+cosx+sinxcosx),
令sinx+cosx=t,则由x∈[0,
],a≠0,可得 t∈[1,
],
且F(x)=
(t+1)2+1-a,
若a>0,则当t=1时,F(x)取得最小值为a+1.
若a<0,则当t=
时,F(x)取得最小值为
a+1.
| x |
| 2 |
| π |
| 4 |
| x |
| 2 |
| π |
| 4 |
| x |
| 2 |
| π |
| 4 |
| x |
| 2 |
| x |
| 2 |
| π |
| 4 |
| x |
| 2 |
=
1+cos(x-
| ||
| 2 |
| 1-cosx |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |
∴函数f(x)的周期为
| 2π |
| 1 |
(2)∵x∈[0,
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| ||
| 2 |
∴f(x)∈[
| 1 |
| 2 |
| ||
| 2 |
(3)将f(x)的图象向右平移
| π |
| 4 |
| 1 |
| 2 |
纵坐标伸长到原来的
| 2 |
F(x)=2af(x)+
| a |
| 2 |
| 2 |
| π |
| 4 |
| a |
| 2 |
令sinx+cosx=t,则由x∈[0,
| π |
| 4 |
| 2 |
且F(x)=
| a |
| 2 |
若a>0,则当t=1时,F(x)取得最小值为a+1.
若a<0,则当t=
| 2 |
2
| ||
| 2 |
点评:本题主要考查函数y=Asin(ωx+φ)的周期性,正弦函数的定义域和值域,函数y=Asin(ωx+φ)的图象变换规律,三角恒等变换以及二次函数的性质应用,体现了转化以及等价转化的数学思想,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 已知直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=
已知直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=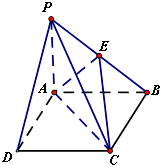 在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点,
在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点, 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA⊥底面ABCD,且SA=2,AD=DC=1,点E在SD上,且AE⊥SD.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA⊥底面ABCD,且SA=2,AD=DC=1,点E在SD上,且AE⊥SD.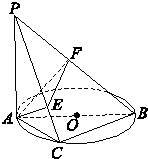 如图所示,已知PA⊥⊙O所在平面,AB是⊙O的直径,点C是⊙O上任意一点,过A作AE⊥PC于点E,AF⊥PB于点F,求证:
如图所示,已知PA⊥⊙O所在平面,AB是⊙O的直径,点C是⊙O上任意一点,过A作AE⊥PC于点E,AF⊥PB于点F,求证: