题目内容
已知f(x)=
x3+x2-3x+1
(Ⅰ)求曲线y=f(x)在(2,f(2))处的切线方程.
(Ⅱ)求y=f(x)的单调递增区间.
| 1 |
| 3 |
(Ⅰ)求曲线y=f(x)在(2,f(2))处的切线方程.
(Ⅱ)求y=f(x)的单调递增区间.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:
分析:(Ⅰ)先求出f′(x)=x2+2x-3,从而f′(2)=5,又f(2)=
,进而求出切线方程,(Ⅱ)令f′(x)>0,则x2+2x-3>0,解不等式即可求出单调递增区间.
| 5 |
| 3 |
解答:
解:(Ⅰ)∵f(x)=
x3+x2-3x+1,
∴f′(x)=x2+2x-3,
∴f′(2)=5,
又f(2)=
,
∴所求切线方程为:y-
=5(x-2),
即:15x-3y-25=0,
∴曲线y=f(x)在(2,f(2))处的切线方程.
(Ⅱ)令f′(x)>0,
则x2+2x-3>0,
解得:x<-3,或x>1,
∴函数y=f(x)的增区间为:(-∞,-3),(1,+∞).
| 1 |
| 3 |
∴f′(x)=x2+2x-3,
∴f′(2)=5,
又f(2)=
| 5 |
| 3 |
∴所求切线方程为:y-
| 5 |
| 3 |
即:15x-3y-25=0,
∴曲线y=f(x)在(2,f(2))处的切线方程.
(Ⅱ)令f′(x)>0,
则x2+2x-3>0,
解得:x<-3,或x>1,
∴函数y=f(x)的增区间为:(-∞,-3),(1,+∞).
点评:本题考察了函数的单调性,导数的应用,求切线方程问题,本题是一道基础题.

练习册系列答案
相关题目
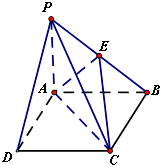 在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点,
在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点,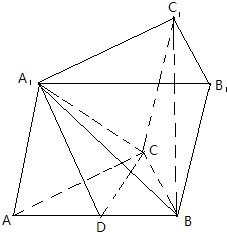 如图,在三棱柱ABC-A1B1C1中,AA1⊥BC,∠A1AC=60°,AA1=AC=BC=1,A1B=
如图,在三棱柱ABC-A1B1C1中,AA1⊥BC,∠A1AC=60°,AA1=AC=BC=1,A1B= 已知一几何体的三视图如图所示,点F,G分别为AC,DE的中点.
已知一几何体的三视图如图所示,点F,G分别为AC,DE的中点.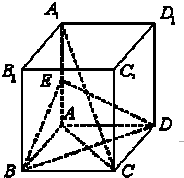 如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点.
如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点.